Hallo,
Wie kommt diese drei "1/N" in den gelben Kreisen raus?
Müssen sie nicht N^-2/N^-2 sein?
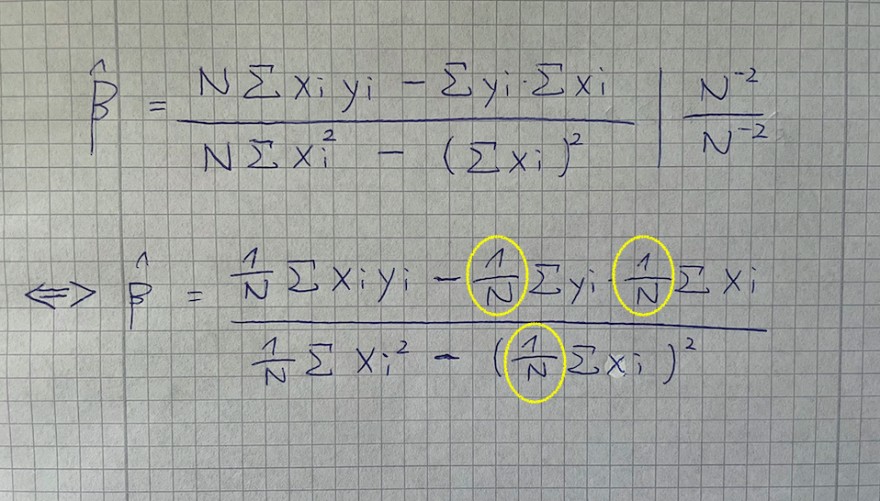
Text erkannt:
β^=N∑xiyi−Σyi⋅∑xiNΣxi2−(∑xi)2∣N−2N−2 \hat{\beta}=\frac{N \sum x_{i} y_{i}-\Sigma y_{i} \cdot \sum x_{i}}{N \Sigma x_{i}^{2}-\left(\sum x_{i}\right)^{2}} \mid \frac{N^{-2}}{N^{-2}} β^=NΣxi2−(∑xi)2N∑xiyi−Σyi⋅∑xi∣N−2N−2⇔β^=1N∑xiyi−(1N)∑yi(1N)∑xi1NΣxi2−(1NΣxi)2 \Leftrightarrow \hat{\beta}=\frac{\frac{1}{N} \sum x_{i} y_{i}-\left(\frac{1}{N}\right) \sum y_{i}\left(\frac{1}{N}\right) \sum x_{i}}{\frac{1}{N} \Sigma x_{i}^{2}-\left(\frac{1}{N} \Sigma x_{i}\right)^{2}} ⇔β^=N1Σxi2−(N1Σxi)2N1∑xiyi−(N1)∑yi(N1)∑xi
Ich hoffe auf Ihre Antwort
Hallo
a*b*n-2=a*n-1*bn-1=1/n*a*1/n*b
und unten steht ja das 1/n in der ()2
Gruß lul
mit dem 1/n im Zähler bin ich klargekommen aber noch nicht ganz mit dem im Nenner.
Ist es sozusagen 1/n*Σxi * 1/n*Σxi = 1/n2(Σxi)2?
Habe ich das richtig verstanden?
Ja. warum ist das nicht klar? mit ∑xi=a=b
lul
jetzt habe ich das verstanden! Es war sehr hilfreich danke schön.
1N \frac{1}{N} N1 ·1N \frac{1}{N} N1=N-2.
Vielen Dank!
Ein anderes Problem?
Willkommen bei der Mathelounge! Stell deine Frage einfach und kostenlos
