Bestimmen Sie die Funktionsgleichung anhand des Flächeninhaltes

Question

Aufgabe: Ein Graph mit einem Flächeninhalt von 36 und die Schnittpunkte bei x=12 und x=0 und der Graph steigt von y=0 zu y=9 wie kann man die Funktion hierzu berechnen ?

Problem/Ansatz: ich verstehe nicht wie ich dort vorgehen soll, weil in der Aufgabenstellung steht: Es handelt sich um eine nicht maßstäbliche Skizze einer Parabel. Bestimmen Sie deren Funktionsgleichung.

Comments

er Graph steigt von y=0 zu y=9

Wie ist diese Aussage zu interepretieren, dass der Hochpunkt bei (6|9) liegt?

---

die Schnittpunkte bei x=12 und x=0

Welche zwei Linien schneiden sich bei $x=12$?

Welche zwei Linien schneiden sich bei $x=0$?

Wie lauten die $y$-Koordinaten der Schnittpunkte?

---

Ein Graph mit einem Flächeninhalt von 36

Und wie lautet die Aufgabenstellung im Original? Ich zweifle, dass das wörtlich so dort steht.

---

Es handelt sich um eine nicht maßstäbliche Skizze einer Parabel. Bestimmen Sie deren Funktionsgleichung. Der x-Wert ist I statt 12

---

Deine Aufgabe ist immer noch unverständlich.

---

Es handelt sich um eine nicht maßstäbliche Skizze einer Parabel. Bestimmen Sie deren Funktionsgleichung. Der x-Wert ist I statt 12

Damit hast du maximal eine der fünf Fragen beantwortet.

---

Die Fragestellung ist immer noch unvollständig.

---

Da bleibt wohl nur noch die Glaskugel oder der Kaffeesatz.

Wieder ein Grund für eine handgebrühte Tasse Kaffee. :)

---

Ich verstehe das so:

Scheitelform der Parabel:

f(x)=a*(x-0,5)²+9=a*x²-ax+0,25a+9

36=$\int\limits_{0}^{1}$(a*x^2-ax+0,25a+9)*dx=$\frac{a}{3}$*x^3-$\frac{a}{2}$*x^2+0,25a*x+9x

36=$\frac{a}{3}$-$\frac{a}{2}$+$\frac{a}{4}$ +9

a=324

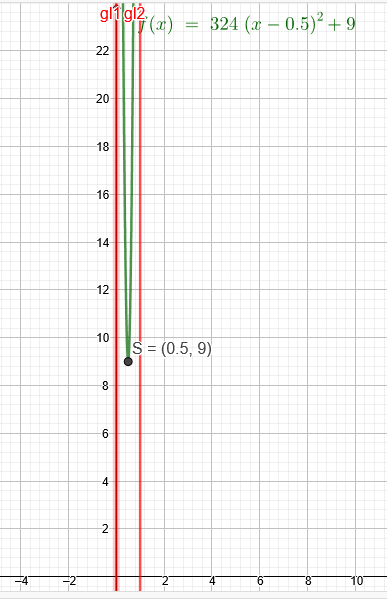
f(x)=324*(x-0,5)²+9

---

Das ist die Funktion

---

1. 2cv, hör doch einmal auf im Forum den
Sheriff zu spielen. Das geht mir so langsam
auf den Keks.

Parabel
( 0 | 0 )
( 6 | 9 )

f ( x ) = ax² + bx + c
f ´ ( x ) = 2ax + b

f ( 0 ) = 0
f ( 6 ) ) 9
f ´ ( 6 ) = 0

geht gleich weiter

---

f ( x ) = -0,25*x² + 3*x

S ( x ) = -0.25 * x³ / 3 + 3 * x² /2
S zwischen 0 und 12

Es kommt bei mir allerdings
A = 72 heraus

---

$f(x) = ax^2 + bx + c;$

Gleichungsystem:

        $\begin{aligned}f(0) &= 0\\f(u) &= 0\\\int\limits_0^u f(x)\,\mathrm{d}x&=36\\ f\left(\frac{u}{2}\right)&=9\end{aligned}$

Lösung:

        $a=-1,b=6, c=0, u=6$

Also

        $f(x) = -x^2 + 6x$

---

Hallo Oswald,

angegeben ist aber
" Schnittpunkte bei x=12 und x=0 "
u ist wie in der Skizze eingetragen bei x = 12

mfg Georg

---

Ich weiß, habe ich auch gelesen.

Meine Glaskugel sagt mir aber etwas anderes. Und die ist immerhin frisch aus der Reparatur gekommen.

---

Wenn man ein Koordinatensystem über das Bild legt,

erkennt man, dass die Funktionsgleichung etwa y = -1,1x²+6,4x sein wird, jedenfalls ist y_s deutlich größer als 9.

---

Update : Ich habe die Verzerrung noch ein wenig korrigiert und zusätzlich die Parabel f mit der Nullstelle N = (5,8 | 0)  und dem Scheitelpunkt S = (2,9 | 9,3)  eingezeichnet.

 

---

Tja. Wie gebogene Buchseiten doch täuschen können. Da mir das Buch von Bigalke/Köhler vorliegt, aus dem diese Aufgabe stammt, kann ich versichern, dass der Scheitelpunkt in einer Höhe von y = 9 liegt.

Wie kann man nur auf die Idee kommen hier einfach eine y-Koordinate anhand einer verzerrten Abbildung zu schätzen?

---

@Georg: Wenn ich richtig gezählt habe, haben sieben Benutzer versucht, der Fragestellerin die Frage zu entlocken. Da kann man getrost davon ausgehen, dass sie nicht mehr an einer Antwort interessiert ist.

---

Nach Kommentaren von 5 Benutzern hat die Fragestellerin eine Grafik eingestellt.
Das kann man als Normalreaktionszeit an-
sehen.
Es gab schon längere Reaktionszeiten sowohl
vom Fragesteller als auch von den
Antwortenden.

Answer 1

Der Scheitelpunkt befindet sich in einer Höhe von h = 9.

Da sich die Fläche unter einer Parabel mit A = 2/3 * g * h berechnen lässt wäre g dann einfach 6

Die Funktionsgleichung lautet demnach einfach y = 9 - (x - 3)² = 6·x - x²