Brüche, das Ganze einzeichnen

Question

Aufgabe:

das Ganze zeichnen

Problem/Ansatz:

Man soll das Ganze von diese Bruchteil zeichnen. Das ist Mathe 5 Klasse. Ich kann mir nicht vorstellen, dass Kind 1/5 von Kästchen einzeichnen soll...

Text erkannt:

\begin{tabular}{|l|l|l|l|}
\hline & \( \frac{5}{12} \) & & \\
\hline
\end{tabular}

Text erkannt:

\begin{tabular}{|l|l|l|l|}
\hline & \( \frac{5}{12} \) & & \\
\hline
\end{tabular}

Comments

wie lautet die Aufgabenstellung genau? Und was ist das 'Ganze'?

---

Wie kann das Ganze aussehen? - das ist Aufgabe.

Normaleweise kann man leicht 1/5 finden und dann fehlende Kästchen zeichen.

Aber hier ist das Ganze 24 Kästchen und 2/5? Wie soll das 5Klässler zeichnen?

---

Streng genommen geht es hier nicht um Fünftel sondern um zwölftel.

---

Lösung soll grafisch sein.

Wie sieht es aus?

---

Aber hier ist das Ganze 24 Kästchen und 2/5?

ich habe die Aufgabe immer noch nicht sicher verstanden! Wenn das oben im Bild \(5/12\) sein sollen, so ist das ganze doch $$11\,\text{Kästchen} \cdot \frac{12}{5}= \frac{132}{5}\,\text{Kästchen}$$oder?? wieso dann 24+2/5?

---

Das ist zwar eine schöne Aufgabe, aber für eine 5. Klasse ungeeignet.

Answer 1

Ich habe mal eine erklärende Zeichnung eingefügt:

Comments

Ich merke jetzt auch, dass mein Weg nicht stimmt. Finde aber im Moment keine passende Lösung.

Answer 2

5/12 -- 11 Kästchen

1 = 12/12 --- 11/5*12 = 26,4 Kästchen

Comments

Danke. Das ist mir klar.

Wie soll es grafisch aussehen?

2/5 lchen von Kästchen zeichnen?

---

Wie soll es grafisch aussehen?

Eine Lösung könnte so

aussehen, würde vom Lehrer aber wohl schnell als nicht aus der Feder eines Fünftklässlers geflossen entlarvt werden.

Answer 3

Zu einem Rechteck mit 11×2 Kästchen ergänzen. Das sind dann \(\frac{10}{12}\) des Ganzen.

Das Rechteck in 5 gleich große Teile aufteilen (n. b. das Rechteck ist 55 mm lang, was man in der fünften Klasse wissen sollte).

Ein solches Teil zu dem Rechteck hinzufügen.

Answer 4

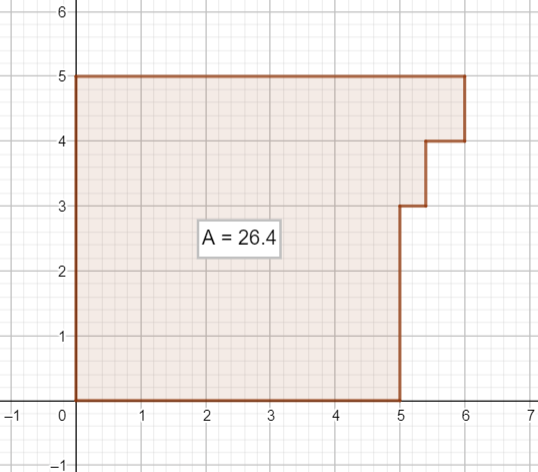
11 sind 5/12 vom Ganzen. Gesucht ist der Grundwert

11 / (5/12) = 11 * 12/5 = 132/5 = 26 2/5 = 26,4

Es gibt jetzt vielfältige Möglichkeiten dies zu skizzieren. Bei mir würde das einfach wie folgt aussehen. Soweit die Bruchrechnung bereits in der 5. Klasse durchgenommen worden war sollte das auch für einen 5. Klässler machbar sein. Dabei konnen durchaus auf Kästchenpapier 0,4 cm abgemessen werden.