Hallo liebe Community,
Ich habe gerade ein Problem, welches ich schon seit zwei Stunden zu lösen versuche.
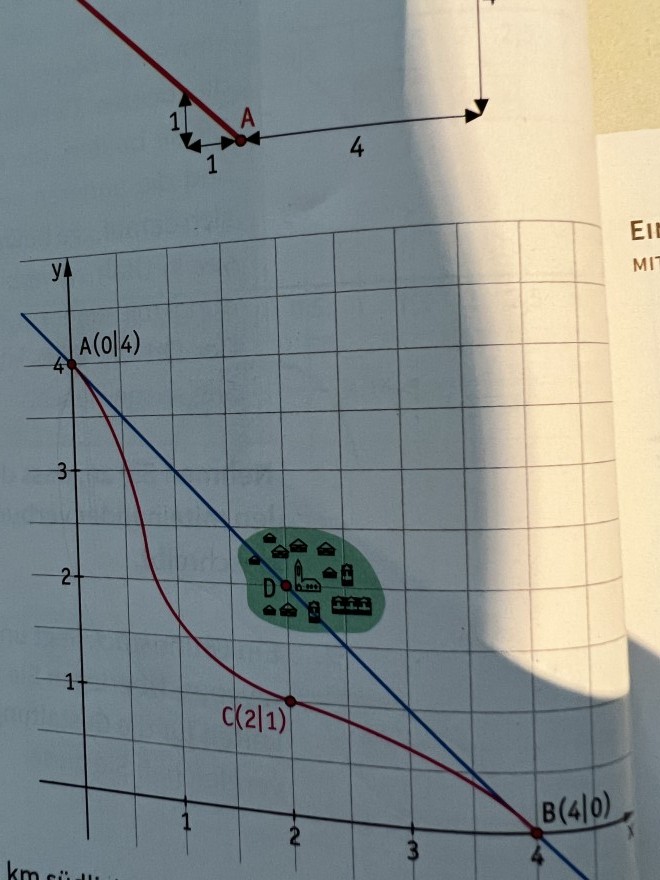
Man hat dieses gegeben Punkte und soll eine Umgehungsstraße planen, welche durch den Punkt A(0|4), den Punkt C(2|1) und durch den Punkt B(4|0) verläuft. Dies habe ich mit einer Funktion 6. Grades gelöst, bis hier hin ist also alles gut… :))
Jetzt soll ich aber zwei ganzrationale Funktionen 4. Grades finden, welche das Gleiche beschreiben. Die eine Funktion soll von A nach C und die andere von C nach B verlaufen. Die Punkte A, C und B müssen alle sprungfrei, knickfrei und krümmungsruckfrei sein.
Ich habe nun zum Einen das Problem, dass ich Steigung, sprich die erste Ableitung von C nicht kennen und zum Anderen das Problem, dass ich pro Funktion 4. Grades 6 Bedingungen habe und so das Gleichungssystem nicht gelöst kriege.
Ich hoffe auf eine gute Antwort !
Liebe Grüße
Vladimir