Zeichne den Graphen der angegebenen Funktion

Question

Aufgabe:

Zeichne den Graphen der angegebenen Funktion. Ermittle anhand des Graphen, an welche Stellen die Funktion den angegebenen Funktionswert annimmt.

a) y= (x-2,5)²+3  Funktionswert: 12

b) y= (x+5)²-9     Funktionswert: -2,75

Problem/Ansatz:

Wie löse ich a) und b)?

Answer 1

Hallo,

a) die Normalprabel wird um 2,5 Einheiten nach rechts und um drei Einheiten nach oben verschoben. Verwende eine Parabel-Schablone, sofern du eine hast. Mit Geogebra sieht das so aus:

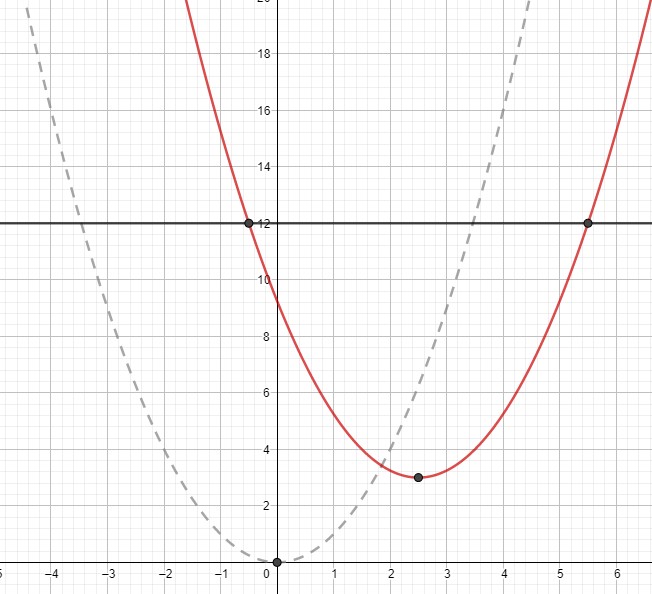
Funktionswert = 12: Ziehe eine zur x-Achse senkrechte Linie in der Höhe von y = 12. Die Schnittstellen von Graph und Linie sind die gesuchten x-Werte.

b) Die Normalparabel wurde um 5 Einheiten nach links und 9 Einheiten nach unten verschoben.

Die weiteren Lösungsschritte sind die gleichen wie in Aufgabe a).

Gruß, Silvia

Answer 2

Kontrolle der zeichnerischen Lösung über eine Rechnung:

a) y= (x-2,5)^2+3  Funktionswert: 12

\(12=(x-2,5)^2+3\)

\((x-2,5)^2=9|\sqrt{~~}\)

1.) \(x-2,5=3\)

\(x₁=5,5\)

2.) \(x-2,5=-3\)
\(x₂=-0,5\)