Verkettung zweier Drehungen

Question

Aufgabe: Verkettung zweier Drehungen

Die Verkettung zweier Drehungen, für die die Summe der Drehwinkel von 360° verschieden ist, ist wieder eine Drehung. Beweise dies und zeige wie man das Drehzentrum und den Drehwinkel der Verkettung konstruieren kann.

Problem/Ansatz:

Liebe Leute,

ich wäre sehr froh, wenn mir jemand bei dieser Aufgabe helfen könnte. Weiss wieder mal nicht wo anfangen und wie ich vorgehen kann. Wenn jemand die Aufgabe anhand einer passenden Figur(Skizze) erklären könnte, würde ich das sehr schätzen, damit ich mir was konkretes vorstellen kann. Vielen herzlichen Dank im Voraus!

Comments

Eine Drehung ist die Verkettung von zwei Geradenspiegelungen.

---

genau, so weit verstehe ich die Aufgabe.

Aber wie kann ich den Drehwinkel und Zentrum konstruieren?

---

>anhand einer passenden Figur(Skizze)<

auf welchen Auschaungsraum beziehst Du Dich?

---

Aber wie kann ich den Drehwinkel und Zentrum konstruieren?

So :

Die Figur F1 wird zunächst um den Punkt A um den Winkel α gedreht, anschließend wird die Bildfigur F2 um den Punkt B um den Winkel β gedreht, was zur Bildfigur F3 führt.

F3 erhält man aus F1 durch eine einzige Drehung um den Punkt C, denn die Drehung um A ist die Nacheinenderausführung der Spiegelungen an den Geraden a (Zwischenbild G) und c, die sich im Winkel α/2 schneiden, die Drehung um B anschließend die Spiegelung an den Geraden c (damit sind wir wieder bei G) und b. Bei diesen vier Spiegelungen heben sich die beiden an c auf, so dass die Spiegelungen an a und b verbleiben, und das ist genau eine Drehung um ihren Schnittpunkt C.

---

Danke sehr, sehr hilfreich!

Answer 1

Scheint mir a weng aufwändig über Spiegelungen zu gehen. Wenn Urbild und Bild gegeben sind, dann finde ich den Drehpunkt über den Schnittpunkt der Mittelsenkrechten zwischen Urbild- und Bildpunkte.

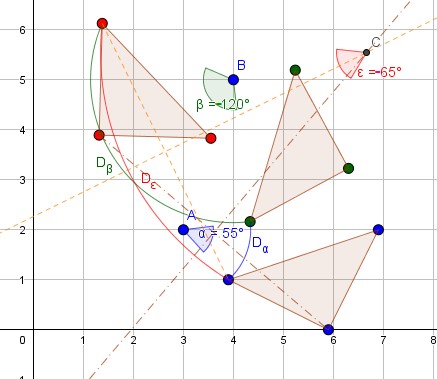
ε = α + β

Rechnerisch sind Drehungen durch Matrizen beschrieben

\(\small D(\alpha) = \left( \begin{array}{rr}\operatorname{cos} \left( \alpha \right)&-\operatorname{sin} \left( \alpha \right)\\\operatorname{sin} \left( \alpha \right)&\operatorname{cos} \left( \alpha\right)\\\end{array}\right) \)

\(\small D(α)D(β) =\left(\begin{array}{rr}\operatorname{cos} \left( \alpha \right) \; \operatorname{cos} \left( \beta \right) - \operatorname{sin} \left( \alpha \right) \; \operatorname{sin} \left( \beta \right)&-\operatorname{cos} \left( \alpha \right) \; \operatorname{sin} \left( \beta \right) - \operatorname{cos} \left( \beta \right) \; \operatorname{sin} \left( \alpha \right)\\\operatorname{cos} \left( \alpha \right) \; \operatorname{sin} \left( \beta \right) + \operatorname{cos} \left( \beta \right) \; \operatorname{sin} \left( \alpha \right)&\operatorname{cos} \left( \alpha \right) \; \operatorname{cos} \left( \beta \right) - \operatorname{sin} \left( \alpha \right) \; \operatorname{sin} \left( \beta \right)\\\end{array}\right)=\\\left(\begin{array}{rr}\operatorname{cos} \left( \alpha + \beta \right)&-\operatorname{sin} \left( \alpha + \beta \right)\\\operatorname{sin} \left( \alpha + \beta \right)&\operatorname{cos} \left( \alpha + \beta \right)\\\end{array}\right)\)

Einbeziehen der Drehpunkte z.B.

\(\left(\begin{array}{rr}\operatorname{cos} \left( \epsilon \right)&-\operatorname{sin} \left( \epsilon \right)\\\operatorname{sin} \left( \epsilon \right)&\operatorname{cos} \left( \epsilon \right)\\\end{array}\right) \left(\vec{x}-C\right) + C\)

oder in homogenen KO bringt man alles in einer Matrix unter...

Comments

1. Meine Konstruktion ist weitaus weniger aufwändig als deine.
Sie bedarf nach Einzeichnen der Verbindungsgeraden von A und B lediglich der Konstruktion zweier Geraden mit jeweils dem halben gegebenen Drehwinkel und Feststellung des Schnittpunktes.

2. Meine Konstruktion ist unabhängig von den Dreiecken.
Kleine Kinder rechnen, indem sie zwei Finger und drei Finger betrachten. Erst später lösen sie sich von den zu addierenden Objekten und rechnen abstrakt 2+3. So solltest auch du dich von den zu drehenden Objekten lösen.

---

Danke für deine Hilfe. Wir mussten aber die Aufgabe (genau wie sie Gast hj2166 gelöst hat) tatsächlich mit/über Spiegelungen lösen.