Geschwindigkeit des Mondes berechnen?

Question

Ich weiß nicht wie man die Geschwindigkeit des Mondes berechnet .

Also ich habe die mittlere Entfernung zur Erde 384400 km und 27,32166 Tage. Mit welchen Fomeln kann man die Geschwindigkeit des Mondes ausrechnen ?

Vielen dank schonmal

PS: weiß nicht ob man wirklich genau DIE oben stehenden Fakten benutzen soll.

Answer 1

  der Mond bewegt sich auf einer Kreisbahn mit dem Radius 384400 km
und der Umlaufzeit 27,32166 Tage.

  Wegstrecke ( Kreis ) = 2 * π * r = 2 * 3.14 * 384400 km
  s = 2.415.256 km

  Strecke = Geschwindigkeit * Zeit
  Geschwindigkeit = Strecke / Zeit
  v = s / t
  v = 2.415.256 km / 27.32166 Tage
  v = 88400 km / Tag
  Dies ist bereits die Angabe der Geschwindigkeit.
  Man kann noch in andere Einhaiten umrechnen
  z.B. km  / Stunde usw.

  Bei Fehlern oder Fragen wieder melden.

  mfg Georg

Comments

Jaa danke schön an alle .  Das hat mir auf jeden Fall weitergeholfen.

Ja, also ich habe die Tage dann in Sekunden umgerechnet,  da  wri ja (fast) immer v= s (meter) / t (sekunde) .

so wäre das dann :

27,32166 Tage * 24 = 655,71984 Stunden * 60= 39343,1904 Minuten * 60 = 2360591,424 --> ca. 2360591 sekunden.

aber ich würde das so machen wie du das gemacht hast, sonst müsste ich ja noch die km-zahl umrechnen ....

Das soll doch 2 Mio 415 Tausend  256 heissen ?

Danke schön :)

Answer 2

 

diese Aufgabe kann man in einer Skizze folgendermaßen darstellen:

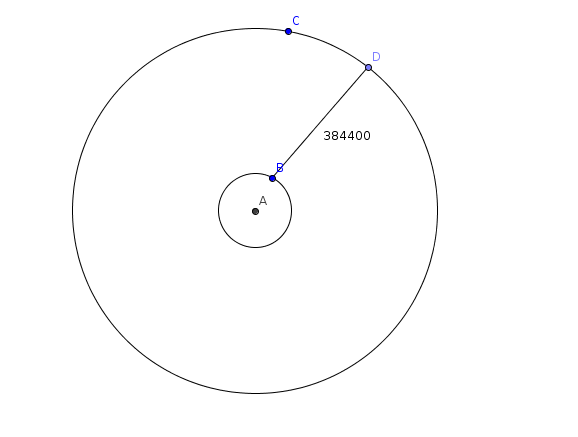
Der Mond "wandert" also einen Kreis entlang, der einen Radius von

384.400km + Radius der Erde hat:

r ≈ 384.400km + 6.371km = 390.771km

 

Der Umfang eines Kreises beträgt

U = 2 * π * r

hier also

2 * π * 390.771km = 2.455.286,60567187km

Für diese Strecke benötigt der Mond 27,32166 Tage = 655,71984 Stunden.

Demnach hat er eine Geschwindigkeit von ca.

2.455.286,60567187/655,71984h ≈

3744,414km/h

 

Er ist demnach noch schneller als mein Roller :-(

 

Besten Gruß

Comments

vielen dank für die antwort ,a ber warum addiert man zu der entfernung den raduis der Erde hinzu ? das habe ich nicht recht verstanden , aber den rest schon :)

---

Gern geschehen :-)

Nun, ich denke, dass der Mond eine Kreisbahn zurücklegt, deren Mittelpunkt der Mittelpunkt der Erde ist - wie in der Skizze gezeigt.

Dadurch wird der Kreis insgesamt etwas größer.

Stell Dir einmal vor, um eine Kugel von der Größe eines Kürbisses rotiert in 1cm Abstand eine Erbse.

Dann hat die Kreisbahn der Erbse nicht den Radius 1cm, sondern den Radius des Kürbisses + 1cm.

Ich fand diesen Ansatz logisch, was meinst Du?

:-)

---

ach soo :D danke nochmal für das Besipiel :)

Jetzt habe ich es verstanden :)
Du scheinst  dich mit dem Thema sehr gut auszukennen , darum habe ich noch eine kleine (Mond-) Frage :

Stimmt diese Behuaptung von mir ?

Der Mond dreht sich um die Erde, da die Erdanziehungskraft der Erde den Mond anziehen und durch gewisse Drehungen des Mondes entstehen sog. Fliehkräfte. Diese entgegengesetzten wirkenden Kräfte wirken, sodass der Mond auf seiner Bahn bleibt.

Vielen dank schonmal .

---

Freut mich sehr, dass Du es verstanden hast !!!


Ich bin wirklich kein Kenner der Astronomie, aber Deine Behauptung stimmt meiner Meinung nach:

Würde der Mond nicht durch die Erde angezogen, würde er durch seine Rotation und die enstehende Fliehkraft in die "unendlichen Weiten des Universums" verschwinden.

Würde er nicht rotieren, so würde er von der Erde angezogen und auf sie stürzen.

Diese beiden entgegengesetzt wirkenden Kräfte sind im Gleichgewicht, so dass der Mond auf seiner Bahn bleibt - Gott sei Dank :-D


Das gilt wohl auch für die Rotation der Erde um die Sonne und unzählige andere Himmelskörper.


Besten Gruß

---

Ich will ja nicht klugsch***en oder so, sondern nur helfen,


aber den Radius noch zum "mittleren Abstand" hinzuzuzählen...^^

Abstände werden immer von Mittelpunkt zu  Mittelpunkt angegeben. Schon alleine stellt sich die Frage bei der Oberfläche von WO man aus misst. Vom Marianengraben oder vom Mount Everest?


Da ich eh schon am Klugschei***en bin (war hier aber idealistisch betrachtet):

Der Mond dreht sich mit der Erde um einen gemeinsamen Schwerpunkt und nicht allein um die Erde. Wegen der größeren Masse fällt das bei der Erde übrigens nicht sonderlich auf. Der Schwerpunk liegt glaube ich sogar unterhalb der Erdoberfläche (und...die Kreisbahn ist selbstverständlich nur eine Näherung).


Grüßle vom KS :P.

---

@Unknown:

Yep, ich war mir ohnehin nicht sicher, ob man nicht auch noch den Durchmesser des Mondes für die Bestimmung des Radius hinzufügen müsste.

Trotzdem glaube ich, dass mein Ansatz ein wenig genauer ist als der der anderen Beobachter ...

Falls nicht, bitte ich dies zu entschuldigen - bin weder Astronom noch Astrophysiker :-)

Wenn man das Ganze auf die Spitze treiben wollte, könnte man ja noch die Rotation der Erde um die Sonne berücksichtigen, die Rotation der Sonne um den Mittelpunkt der Galaxis, und diese wird ja auch noch um irgendein Zentrum kreisen - mir wird schon ganz schwindelig :-D

---

Bevor man die Rotation um andere Himmelskörper berücksichtigt, würde ich erstmal von der Kreisbahn weggehen^^.


Deshalb glaube ich auch nicht, dass Dein Wert genauer ist. Geht ja nicht um den Beobachtungspunkt, sondern um den Meßpunkt. Mal abgesehen davon, dass "Du" als Beobachter nichtmal ein Mittelpunkt eines (bzw. des) Kreises bist.

Ist ja ohnehin nur ein "mittlerer" Abstand (eben wegen der eigentlichen Ellipsenbahn).

Habe gerade mal den Literaturwert nachgeschlagen: 3682,8 km/h

Da liegen die anderen verdammt gut^^.

---

@Unknown:

Ich möchte nicht penetrant sein, aber ich finde diese Aufgabenstellung sehr interessant.

Du hast angegeben:

"Abstände werden immer von Mittelpunkt zu  Mittelpunkt angegeben."

Folgt daraus, dass, wenn man zum Beispiel zwei Kugeln mit einem Radius von jeweils 2 Metern hat und diese beiden Kugeln sich berühren, deren Abstand 4 Meter beträgt?

Klingt konsequent, ist aber m.E. irgendwie kontraintuitiv :-)

---

Verzeih, da war ich vielleicht nicht genau genug.

Bei kosmischen Größen wird das Ganze immer (ich glaube hier ist "immer" ziemlich zutreffend) von Mittelpunkt zu Mittelpunkt zu gehandhabt ;).


(Nicht nur da, auch im Mesokosmos und im Mikrokosmos sowieso, werden auch gerne Mittelpunkt zu Mittelpunktabstände angegeben.)

---

Gut, das leuchtet mir ein.

Danke für Deine Erläuterungen!!


Ich verlasse hiermit kosmische Maßstäbe und ziehe mich auf meine Kurvendiskussionen, Bruchrechnungen, Wurzelvereinfachungen etc. zurück :-)


Dies war ein Scherz, kein Trotzen und Schmollen :-DD

---

  ein Aspekt  wurde glaube ich noch nicht erwähnt : die Mondbahn ist
ellipsenförmig mit einem erdnächsten Abstand von 356.400 km und
dem erdfernsten Abstand von 406.704 km. Also ein recht erheblich
Umstand.

  Die Ellipsenförmigkeit  z.B. der Planentenbahnen um die Sonne wurde
von Joahnnes Kepler als erstem erkannt und berechnet.
mfg Georg

---

Doch hatten wir mehrfach erwähnt, dass hier Kreisbahn idealistisch angenommen wurde ;).

Answer 3

v = s / t = 2 · pi · 384400 / (27.32166 · 24) = 3683 km/h

Answer 4

Wir haben als Formel für die Geschwindigkeit des Mondes aufgeschrieben: 4pi^2*r / T^2 T ist die Umlaufdauer:27,3d =2,36*10^6 s R=386000 km Ich bin mir aber nicht sicher ob es genau das ist, was du brauchst :/

Comments

Mit der Formel V = S : t bekommt man falsche Werte, weil der Mond in Ernähe schneller fliegt und in Erdferne langsamer. Mit dieser Formel bekommt man Werte, dass der Mond in Ernähe langsamer und in Erdferne schneller fliegt, weil der Radius in Erdnähe kleiner ist als in Erdferne. Es fehlt die Fliehkraft. Wie berechne ich also die Fliehkraft des Mondes.