Question

Berechnen Sie den Gradienten zu f: R³-> R, f(x, y, z) = 3x²+5yz² an der Stelle (1, 3, 2) näherungsweise, indem Sie jeweils numerische Ableitungen nutzen, d. h. entsprechende Differenzenquotienten, mit h = 0,1.

grad f(1,3,2) = (  , , )

Answer 1

Hallo

Beispiel f_x (1,2,3)= (3(1+0,1)^2-3)/0,1=6,1

entsprechend du die 2 anderen  also (f(1,2+0,1,3)-f(1,2,3))/0,1 für fy

Gruß lul

Comments

6,1 für x ist falsch!

---

Danke Georg , aber der Ausdruck davor ist noch richtig. ich überlass dem Fragenden das Ausrechnen.

lul

Answer 2

Aloha :)

Du sollst die numerische Ableitung mit \((h=0,1)\) bestimmen.

Die erste Idee ist dann oft, die Ableitung durch den bekannten Differenzenquotienten zu nähern (vgl. die Antwort von lul):$$f'(x)\approx\red{\frac{f(x+h)-f(x)}{h}}$$Das ist aber leider falsch. Die Abweichung dieses Ausdrucks liegt in der Größenordnung \(O(h)\), was hier der ersten Nachkommastelle entspricht.

Die tatsächliche numerische Ableitung hat die Abweichung \(O(h^2)\):$$f'(x)\approx\green{\frac{f(x+h)-f(x-h)}{2h}}$$ Die Genauigkeit liegt damit in unserem Fall bei der zweiten Nachkommstelle, was einer Verzahnfachung der Genauigkeit entspricht.

Ich habe den Gradient numerisch mit beiden Formeln bestimmt:

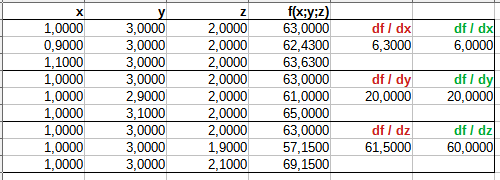
und erhalte als Ergebnis:$$\red{\operatorname{grad}f(1;3;2)\approx\begin{pmatrix}6,3\\20\\61,5\end{pmatrix}}\quad;\quad\green{\operatorname{grad}f(1;3;2)\approx\begin{pmatrix}6\\20\\60\end{pmatrix}}$$

Der tatsächliche, exakte Gradient ist:$$\operatorname{grad}f(1;3;2)=\begin{pmatrix}6\\20\\60\end{pmatrix}$$