Taylorpolynom mit Wert abschätzen

Question

Aufgabe:

Text erkannt:

Gegeben sei die Funktion $f: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \cos (x)$.
(a) Geben Sie das Taylorpolynom zweiten Grades von $f$ in 0 an (also $T_{2, f}(x ; 0)$ ).
(b) Zeigen Sie, dass $\left|\cos \left(\frac{1}{8}\right)-T_{2, f}\left(\frac{1}{8} ; 0\right)\right| \leq \frac{1}{3072}$. (Hinweis: $3072=6 \cdot 8^{3}$ )

Problem/Ansatz:

Mir ist bewusst, dass ich einen Fehler gemacht habe und cos(1/8) und das Taylorpolynom beide nahe eins sind, sodass man einen Wert nahe 0 rausbekommt, wenn man diese subtrahiert. Wie gehe ich nun aber weiter vor? Ich verstehe nicht so ganz, wie mann die Abschätzung dann zum Schluss macht (ohne Taschenrechner natürlich).

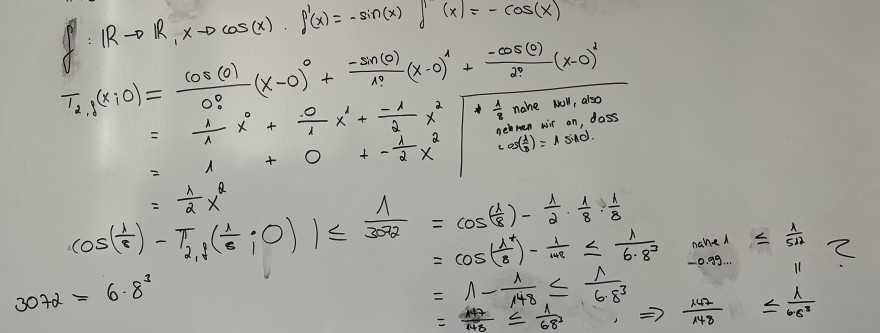
Text erkannt:

$\begin{array}{l}=1+0+-\frac{1}{2} x^{2} \quad \begin{array}{l}\frac{1}{2} \text { ehthen wir an, dass } \\ \cos \left(\frac{1}{8}\right)=1 \text { sind. }\end{array} \\ =\frac{1}{2} x^{2} \\ \left.\cos \left(\frac{1}{8}\right)-T_{2,1}\left(\frac{1}{6} ; 0\right)\right) \leqslant \frac{1}{3072}=\cos \left(\frac{1}{8}\right)-\frac{1}{2} \cdot \frac{1}{8} \cdot \frac{1}{8} \\ =\cos \left(\frac{\Lambda^{*}}{8}\right)-\frac{1}{148} \leq \frac{1}{6 \cdot 8^{3}} \underset{\substack{\text { nahe } \\ \text {-0.99... }}}{\cos } \leq \frac{1}{512} ? \\ 3072=6 \cdot 8^{3} \\ =1-\frac{1}{148} \leq \frac{1}{6 \cdot 8^{3}} \\ =\frac{147}{148} \leq \frac{1}{68^{3}}, 6.8^{3} \Rightarrow \frac{147}{148} \leq \frac{1}{6.8^{3}} \\\end{array}$

Answer 1

Da die Taylorreihe alterniert, ist die Abweichung kleiner als der nächste von 0 verschiedene Summand (und der ist $\frac{x^4}{4!}$).

Answer 2

Hallo

du brauchst die Restgliedabschätzung R3= sup(f'''(ξ))3!*x³ ) das sup im Intervall (0,1/8)

Gruß lul

Comments

Verwendet man immer das Restglied, um Abschätzungen zu machen?

Das heißt, ich würde dann statt T2 dann T3 (also R3) verwenden, um die Abschätzung durchzuführen?

---

hallo

Ja Fehler werden immer mit dem Restglied abgeschätzt, denn das TP benutzt man ja wenn man die Funktionswerte z.B, cos(1/8) nicht kennt,

lul