Bestimmen Sie jeweils den Differenzenquotienten im Intervall I.

Question

Gegeben sind die Funktionen $f$ und $g$ mit $f(x)=0,5 x^{2}$ und $g(x)=3 x^{3}+1$. Bestimmen Sie jeweils den Differenzenquotienten im Intervall I.
a) $I=[0 ; 2]$
b) $\mathrm{I}=[-1 ; 3]$
c) $I=[-1 ; 1]$
d) $I=[-2 ;-1]$

Comments

Was ist Deine Frage dazu? Weißt Du nicht, was ein Differenzenquotient ist und wo man das nachlesen kann?

Answer 1

Hallo,

den Differenzenquotieten = Steigung einer Geraden m kennst du sicherlich noch aus früheren Jahren.

$m=\frac{y_1-y_2}{x_1-x_2}$

Hier machst du das Gleiche. Beispiel Aufgabe a) und f(x)

Die Intervallgrenzen bestimmen die Koordinaten der Punkte. Ich nenne sie A und B.

$A=(0\mid0)\quad B=(2\mid2)$

$m=\frac{0-2}{0-2}=\frac{-2}{-2}$

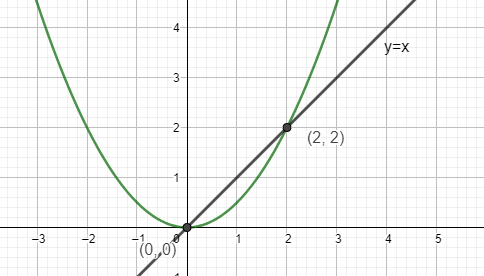
Naja, eine andere Aufgabe wäre zur Veranschaulichung vielleicht besser gewesen. Wenn du noch Fragen hast, dann melde dich.

Gruß, Silvia

Answer 2

Ein Beispiel sollte genügen

I=[−1;3]:  f(3)=9/2 ; f(-1)=1/2

f(3)-f(-1)/(3-(-1))=4/4=1

nach dem Rezept alle

Gruß lul

Comments

f(3)-f(-1)/(3-(-1))=4/4=1

Klammern um den Zähler!

---

Klammern um den Zähler!

Noch besser so:

$\frac{f(3)-f(-1)}{3-(-1)}=\frac{4}{4}=1$

---

Man kann den Leuten leider kein LaTeX aufzwingen... Da gibt es nämlich einige, die das nicht nutzen...

---

Danke für die Verbesserung.

lul