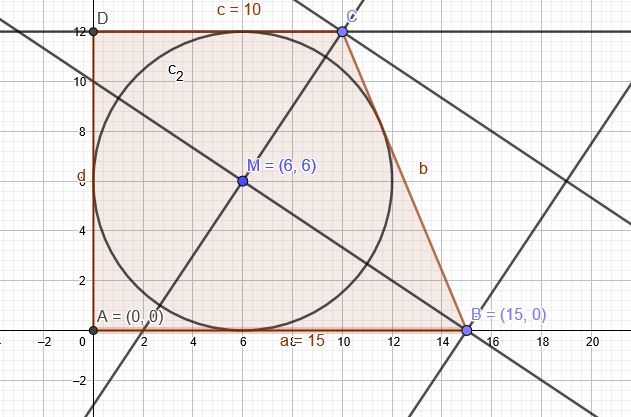
Planfigur:
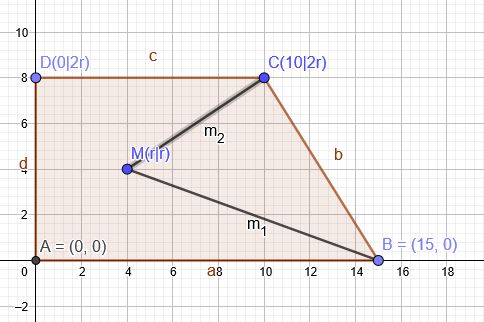
Steigung der Geraden durch B und M:
\( m_1=\frac{r}{r-15}\)
Steigung der Geraden durch C und M:
\( m_2=\frac{r}{10-r}\)
Die Winkelhalbierende durch B geht durch M ebenso die Winkelhalbierende bei C.
Diese stehen senkrecht aufeinander. Die Gerade durch A und B ist parallel zu der Geraden durch C und D. Somit ist der Winkel \(β\) bei B gleich groß wie der Nebenwinkel von \(γ\) bei C.
Somit gilt :
\( \frac{r}{10-r}=\frac{15-r}{r} \)
Aufgelöst ist \(r=6 \)