Aufgabe:
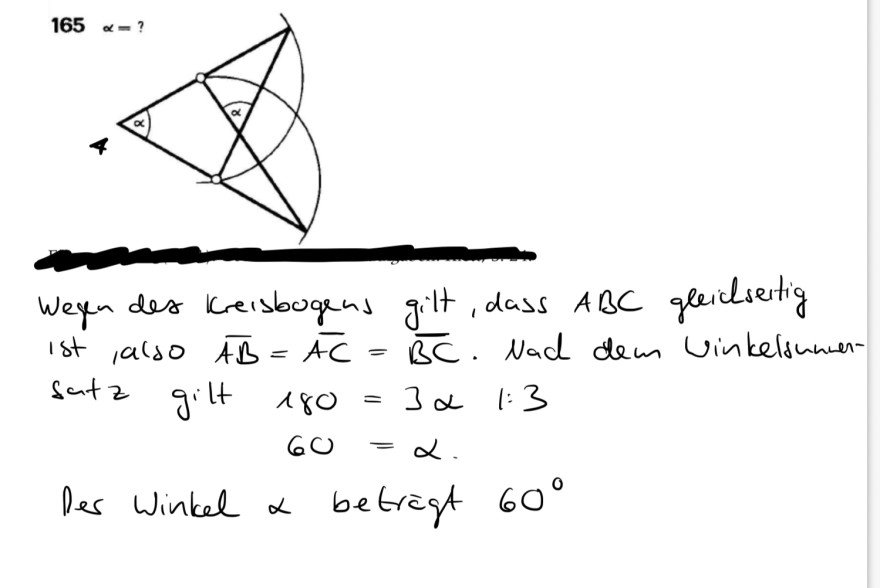
Ohne Taschenrechner; die Figuren sind nicht maßgetreu.
Paul Eigenmann, Aufgabe 1.4.165, ISBN 3-12-722310-2, 1981, S. 24.
Problem/Ansatz:
Text erkannt:
Wegn des kreisbogens gitt, dass \( A B C \) gleidsertig ist, \( 19180 \overline{A B}=\overline{A C}=\overline{B C} \). Nad dem Vinkelsmensatz gilt \( 180=3 \alpha \) 1:3
\( 60=\alpha . \)
Der Winkel \( \alpha \) betrigt \( 60^{\circ} \)
Servus Leute und zwar wollte ich wissen, ob ich diese geometrische Denkaufgabe richtig gelöst habe. Mir erschien es zu einfach….