Eigenmann: Frage 139, 1.Teil

Question

Aufgabe:

Eigenmann : Frage 139, 1.Teil

Problem/Ansatz:

Answer 1

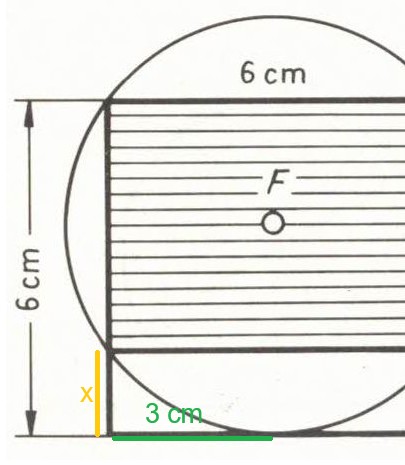
Sekanten-Tangentensatz: x * 6 cm = (3cm)², also x=1,5 cm. Das Rechteck hat dann eine Höhe von (6 cm - 1,5 cm = ) 4,5 cm und einen Inhalt von 27 cm².

Wenn man diesen Satz nicht kennt geht es auch so:

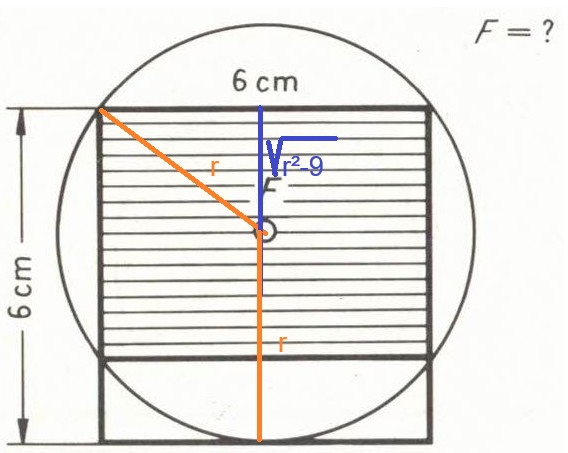
Für den nach unten eingezeichneten Radius gilt

r=6-\( \sqrt{r^2-9} \)

r²-9=36-12r+r²

r=15/4.

Daraus folgt

r²=225/16

r²-9 = 81/16

\( \sqrt{r^2-9}=9/4 \).

Das schraffierte Rechteck hat eine Höhe von (2*2,25 cm =) 4,5cm und eine Fläche von 27 cm².

Answer 2

Wenn \(d\) der Durchmesser des Kreises, \(x\) der Abstand der unteren Rechteckkante zur unteren Quadratkante ist, also \(x=6-y\), wobei \(y\) die kurze Seite des Rechtecks ist, dann gilt aus Symmetriegründen

\(d=y+2x\) und mit Pythagoras \(6^2+y^2=d^2=(y+2x)^2=(12-y)^2\).

Das ist eine lineare Gleichung mit der Lösung \(y=4,5\) und daher ist \(F=27\, (\mathrm{cm}^2)\).

Comments

mit anderen Worten:

Eine Kopie des gelben Rechtecks unten mit der Höhe x passt aus Symmetriegründen  oben zwischen die Fläche F und den höchsten Punkt des Kreises. Die gemeinsame Höhe der drei Rechtecke ist der Kreisdurchmesser
d = 6cm + x.

:

---

Die Höhe von F ist: h = 6 - x .

Der Kreisdurchmesser ist auch die Diagonale der Fläche F .
Im sie enthaltenden rechtwinkligen Dreieck gilt:
d² = 6² + h² bzw. (6 + x)² = 6² + (6 - x)².

Ausgerechnet: x = 3/2  >>  h = 9/2  >>  F = 27 cm² .

---

Auch eine schöne Lösung ...

Answer 3

Ich hätte direkt den Pythagoras formuliert.

3^2 + (6 - r)^2 = r^2 --> r = 3.75 cm

Daraus würde ich dann die Fläche berechnen.

F = 6·2·(6 - 3.75) = 27 cm²