Eigenmann-Aufgabe # 140 im Teil 1

Question

Aufgabe:

Eigenmann-Aufgabe #140 im Teil 1

Answer 1

Kleiner Tipp, weil es nicht explizit in der Aufgabe steht. w ist die Winkelhalbierende. Und die Skizze ist nicht maßstabsgetreu.

Comments

Hier meine Lösung:

[spoiler]

Die gesamte Dreiecksfläche berechnet sich nach dem Satz von Heron aus

s = 1/2 * (130 + 140 + 150) = 210

A_G = √(210 * (210 - 130) * (210 - 140) * (210 - 150)) = 8400 cm²

Diese Fläche wird durch die Winkelhalbierende im Verhältnis 130 : 150 geteilt. Damit beträgt die Fläche des Dreiecks unter der Winkelhalbierenden

A₂ = 8400 * 150/(130 + 150) = 4500 cm²

Daraus kann man jetzt direkt x berechnen.

A₂ = 1/2 * 150 * x = 4500 → x = 60 cm

[/spoiler]

---

Da widersprichst du dir wieder einmal selbst. Der Satz von Heron wird in der von dir höchst selbst verlinkten Formelsammlung nicht erwähnt.

---

Nein. Aber Eigenmann erwähnt die Formel zum Lösen.

Ich könnte es auch ohne die Formel von Heron lösen. Aber das ist natürlich aufwendiger.

Wenn holdi sich also mit den Eigenmann-Aufgaben beschäftigt und dabei Schwierigkeiten hat, sollte man davon ausgehen, dass er sich die Formeln, die als Tipp zur Lösung gegeben sind, notiert hat und/oder vielleicht auch mal versucht hat, diese Formeln mit Schulmathematik herzuleiten.

Answer 2

Planfigur: (nicht maßstabsgetreu)

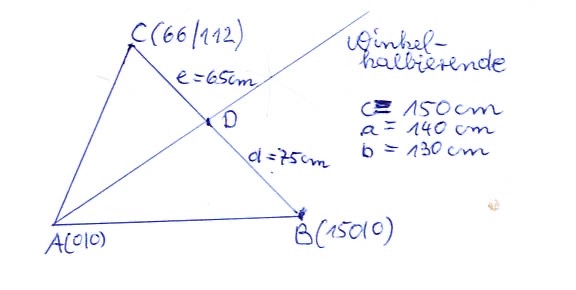
Berechnung von C über den Kreis um A(0I0) mit r=b und Kreis um B(150I0) mit r=a bringt die Koordinaten von C mit C(66I112).

Nun besagt der Winkelhalbierendensatz:

Die Winkelhalbierende des Winkels α teilt die Seite a in demselben Verhältnis wie die anliegenden Seiten b und c zueinander stehen:

b:c=130:150

Bezogen auf die Planfigur bringt das e:b=d:c

Wir erhalten 2 Gleichungen:

1.) e:130=d:150

2.) e+d=140

Aufgelöst ergibt das die in der Planfigur eingetragenen Werte.

Über die Zweipunkteform einer Geraden lässt sich die Geradengleichung durch die Punkte B und C bestimmen.

Der Kreis um B mit r=d schneidet die Gerade in D.

Mit dem y-Wert der Koordinate von D haben wir nun x=? gelöst.

Comments

Woher hast du die Koordinaten von C?

Nachträglich stellt man fest, dass tatsächlich 66²+112²=130² ist.

Aber das ist nur die Probe für deine Koordinaten, die anscheinend vom Himmel gefallen sind.

---

Woher hast du die Koordinaten von C?

1.) Kreis um A(0I0) mit r=b   →   x^2+y^2=130^2

2.). Kreis um B(150I0) mit r=a    →  (x-150)^2+y^2=140^2

 1.) auflösen nach y^2→  y^2=130^2-x^2 dann einsetzen in 2.):

(x-150)^2+130^2-x^2=140^2

x^2-300x+150^2+130^2-x^2=140^2

-300x+150^2+130^2=140^2

-300x=140^2-150^2-130^2=-19800

x=66   Nun einsetzen in y^2=130^2-x^2→ y^2=130^2-66^2=12544

y_1=112

y_2=-112 (entfällt)

C(66I112)