1,5^x + 3 =2^x Wie kann man diese Gleichung lösen? Vielen Dank vorab!

Question

1,5^x   +   3    =   2^x

Wie groß ist x?

Mit den normalen Logarithmjsgesetzen schaffe ich die Aufgabe leider nicht. Bitte um Hilfe :)

Answer 1

das wirst Du mit einem Näherungsverfahren lösen müssen. Das Newtonverfahren bietet sich hier eventuell an:

https://www.mathelounge.de/49035/mathe-artikel-das-newtonverfahren

Ich komme auf x ≈ 2,535

Grüße

Answer 2

Hallo

kannst Du nur mit Näherungsvefahren (z.B.) von Newton lösen.

Ergebnis: x =2.53475( rund)

Answer 3

1.5^x + 3 = 2^x

Algebraisch ist das mit der Schulmathematik nicht möglich. Dort verwendet man dann meist ein Näherungsverfahren.

1.5^x - 2^x + 3 = 0 --> x = 2.534754731

Answer 4

Du schreibst leider nicht, welche Klassenstufe  :-(

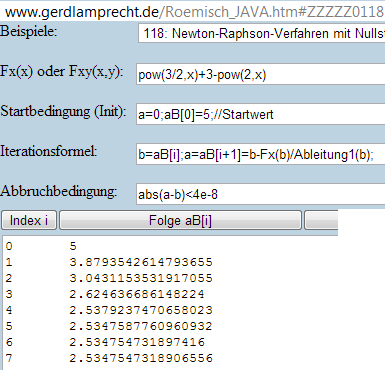
Newton-Verfahren (siehe Wikipedia oder http://www.gerdlamprecht.de/Roemisch_JAVA.htm#ZZZZZ0118

Beispiel 118 mit Formel Fx: pow(3/2,x)+3-pow(2,x)  ) kommt erst nach dem Abi...

Ich vermute, dass Klammer fehlt:

(3/2)^{x+3}=2^x  denn das kann man mit dem Gesetz

x^a = pow(x,a) = e^{log(x)*a}=exp(log(x)*a) umstellen

{ergibt x=(log(27/8))/(log(4/3)) }

denn

(3/2)hoch((log(27/8))/(log(4/3))+3)-2hoch((log(27/8))/(log(4/3))) = 0 

(musste hoch statt ^ schreiben, weil der Editor sonst den Hoch-Teil mitten in der Gleichung in normale Höhe wechselt)