Lösen einer schwierigen Logarithmusaufgabe

Question

$$ \frac { 1 }{ c1 } * (-log(|1-(x-h1)|)) = \frac { 1 }{ c2 } * (-log(|1-(x-h2)|)) $$

x ist gesucht. Logarithmus ist zur basis b

Comments

Rechne erst mal 

"Mal -c1*c2"

So verschwinden die Brüche und die beiden Minus vor den log.

EDIT: Was meinst du mit "komplex"? Komplexe Zahlen? 

---

Komplex im Sinne von schwer :-)
c2* log(|1-(x-h1)|) = c1*(log(|1-(x-h2)|)
c2* ln(|1-(x-h1)|)/ln(b) = c1*(ln(|1-(x-h2)|)/ln(b) 
wie gehts nun weiter?

---

c2* log(|1-(x-h1)|) = c1*(log(|1-(x-h2)|)        ln brauchst du nicht. Log-gesetze benutzen

 log((|1-(x-h1)|)^{c2}) = log((|1-(x-h2)|)^{c1} )      | beidseitig b^.... ==> log ist weg.

(|1-(x-h1)|)^{c2} = (|1-(x-h2)|)^{c1}         

nun bist du so weit, wie georgborn.

Allzu viel kannst du da nicht mehr machen. wenn du willst: Fallunterscheidung, um Beträge wegzubringen.

Wurde dir diese Gleichung so gegeben? 

---

Die Lösungen muss ich für verschiedene h1,h2,c1,c2 möglichst effizient lösen. Man kann das wohl nur noch mit dem Newtonverfahren approximieren. Kann einer noch meine Ableitung verifizieren?

1/(|1-x+h|*c)

Answer 1

Vielleicht helfen dir die Umformungen schon einmal weiter.

Comments

Danke, soweit hatte ich es auch hinbekommen. Die Frage stellt sich nun ob man das nur approximieren (beispielsweise newtonverfahren) kann oder sich das noch vereinfachen lässt.

---

Allgemein kann ich die Gleichung nicht nach x umstellen.
Mein Matheprogramm auch nicht.

Sind h1,c1,h2,c2 konkret gegeben  lassen sich die Lösungen
wohl finden.
z.B. Linke und rechte Seite der Gleichung als Graph zeichnen,
den Schnittpunkt ermitteln oder/und Newton-Verfahren anwenden.

ich kann das gerne bei Bedarf einmal vorführen.

---

Danke dir georg, mir fehlt eigentlich nur noch die Ableitung für die Funktion.

Meine ermittelte ist: 1/(|1-x+h|*c). Die scheint aber nicht ganz richtig zu sein.

---

Meinst du jetzt die Ableitung für

(  | 1- x + h | ^c  ) ´

Diese wäre für
( 1 - x + h ) > 0

c * ( 1 - x + h ) ^{c-1} * ( -1 )
-c * ( 1 - x + h ) ^{c-1}

---

Stimmt.. für die Vereinfachte Version is die Ableitung wohl einfacher zu bewerkstelligen

---

Weißt du vielleicht wie HyperG auf: d/dx (|1-(x-h1)|)^c2-(|1-(x-h2)|)^c1 = c1*(1+h2-x)*abs(1+h2-x)^c1-2 - c2*(1+h1-x) abs(1+h1-x)^c2-2 

gekommen ist?

Muss man nicht alle Fälle einzelnd für sich betrachten?

---

Die Antwort von HyperG habe ich mir nicht angeschaut.
Ich hoffe HyperG kann dir noch weiter helfen.

mfg Georg

Answer 2

Natürlich kann man versuchen den exakten Weg zu gehen, ABER da kostet zig Fallunterscheidungen und viel Gefahr von Flüchtigkeitsfehlern, da die Formeln extrem lang werden!

Natürlich kann man mitten drin abbrechen und dann doch auf Näherungsverf. umschalten: 

Für Newton -V. musst Du eine Nullstellenfunktion erstellen

und diese Ableiten:

d/dx (|1-(x-h1)|)^c2-(|1-(x-h2)|)^c1 = c1*(1+h2-x)*abs(1+h2-x)^{c1-2} - c2*(1+h1-x) abs(1+h1-x)^{c2-2}  

Viel kürzer und einfacher ist gleich die Ausgangsfunktion zur Nullstellenfunktion zu wandeln und in den Iterationsrechner Beispiel 118 einzutragen: 

Deine 4 globalen Konstanten c1, c2, h1, h2 habe ich ins Array aC gepackt:  

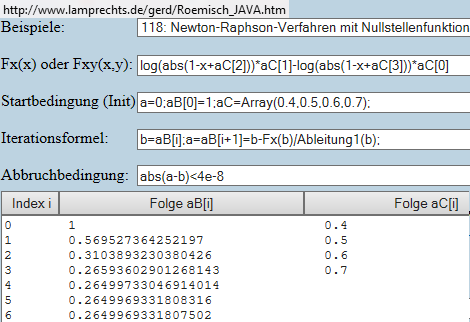
Eingeschwungen (konvergiert) bei b=aB[6]=0.2649969331807502... 

Gibt es Aussagen zu den 4 globalen Konstanten c1...h2 wie reelle Zahlen oder ganze oder komplexe...?

Comments

c1,c2 > 0

h1,h2 in [0,1)

Alles reelle Zahlen

---

Wie kommst du auf d/dx (|1-(x-h1)|)^c2-(|1-(x-h2)|)^c1 = c1*(1+h2-x)*abs(1+h2-x)^c1-2 - c2*(1+h1-x) abs(1+h1-x)^c2-2  

Bist du alle Fälle durchgegangen und hast die daraus dann abgeleitet?

oder gibt es eine spezielle Regel die alle Fallunterscheidungen überflüssig macht?. Anscheinend bekommt man ja durch die (1+h2-x) terme das Signum?

---

In diesem Falle habe ich WolframAlpha zum Ableiten verwendet.

Und da für alle 3 Lösungswege das selbe herauskam, scheint es auch zu stimmen:  

Lösungsweg 2 "umgestellte Funktion mit numerischer Ableitung":  

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#@P@A1-(x-@C2])),@C1])-@P@A1-(x-@C3])),@C0])@Na=0;@B0]=1;aC=Array(0.4,0.5,0.6,0.7);@Nb=@Bi];a=@Bi+1]=b-Fx(b)/@Lb);@N@Aa-b)%3C4e-8@N1@N0@N#  

kommt auch 0.26499693318075... heraus  

Lösungsweg 3: "umgestellte Gleichung + symbolische Ableitung"

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#@P@A1-(x-@C2])),@C1])-@P@A1-(x-@C3])),@C0])@Na=0;@B0]=1;aC=Array(0.4,0.5,0.6,0.7);@Nb=@Bi];a=@Bi+1]=b-Fx(b)/(@C0]*(1+@C3]-b)*@P@A1+@C3]-b),@C0]-2)%20-%20@C1]*(1+@C2]-b)*@P@A1+@C2]-b),@C1]-2));@N@Aa-b)%3C4e-11@N1@N0@N#  

kommt auch 0.26499693318075...   

Das meinte ich damit: warum erst umstellen und komplizierte Ableitungen mit Sonderfallbehandlungen, wo man gleich die Ausgangsgleichung nehmen kann!

Ist doch bereits eine numerische Näherung mit der Double-Genauigkeit von 14 Nachkommastellen.   

Die ganze Umstellerei für Lösungsweg 2 und 3 wird damit auch nicht genauer (aber fehleranfälliger)! 

---

Hier mal eine Sonderfallbehandlung für ganzzahlige Werte c1=2 und c2=3:

Wer da keine Fehler macht.... muss schon perfekt sein...   

Für "krumme Werte" nicht mehr so einfach...

Die vielen Operationen und Funktionen senken die Genauigkeit des Endergebnisses weiter:   

Wer schon mal Fehlerfortpflanzung genauer untersucht hat, kann das verstehen.

(ich hatte mal eine Formel die ich auf über 200 Nachkommastellen berechnen musste, damit das Endergebnis auf 2 Stellen stimmte) 

---

Ich würde gerne wissen wie Wolframalpha auf die Ableitung kommt. Die Ableitung scheint ja korrekt zu sein. Die Lösung ist so schön einfach ( c1*(1+h2-x)*abs(1+h2-x)^c1-2 - c2*(1+h1-x) abs(1+h1-x)^c2-2  ). Keine Fallunterscheidung nötig. Wäre cool wenn mir das einer erklären könnte, wie man darauf kommen kann

---

Du brauchst nur den Teil betrachten:

d/dx abs(a-x)^b = b*(x-a)*abs(a-x)^{b-2}  

Der Faktor (x-a) sorgt bereits für Vorzeichenwechsel.

Das kann man sich auch bei der numerischen Ableitung unter 

http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm  

mit pow(abs(PI-x),3.9) und Punkte = auto ansehen

Dann ist der Button "Ableitung" aktiviert -> blau gestrichelte Kurve

Habe extra krumme Werte genommen, da glatte wie 2 oder 3 wieder Sonderfälle wären.

---

Oder einfach:

(x-Pi)*abs(Pi-x)^{e-2} = sgn(x-Pi)*abs(Pi-x)^{e-1} 

statt Pi und e hätte ich auch c1 und h1 schreiben können.

Nun verstanden?

---

Durch abs(...)^y  ist es immer eine nach oben offene Parabel - egal welches y. 

(nicht wie bei x^3 , dass negativ oder bei x^{1/2} bei x<0 komplex werden kann)

Die Ableitung bis zum Minimum ist daher immer negativ

im Minimum =0

und danach immer positiv.

---

Also wenn man alle Fälle unterscheiden würde und diese vereinfacht, sieht man durch die Umformung dass man das Vorzeichen durch das rausziehen automatisch bestimmen kann und somit eine Formel erhält die Alle Fälle abdeckt?

Gibt es eine feste Regel die das Umformen von (x-Pi)*abs(Pi-x)^e-2 = sgn(x-Pi)*abs(Pi-x)^e-1   erlaubt oder bekommt man die Vereinfachung indem man das aus dem Kontext "schlussfolgert"?

Den Sinn habe ich ja verstanden, will nur wissen ob es eine feste Regel dafür gibt oder es einfach eine zur Aufgabe individuelle Schlussfolgerung ist.