Ermittle die Höhe des Berges. Von der Spitze eines Berges wurden die Tiefenwinkel alpha=32,3 Grad und beta=39,7 Grad

Question

Von der Spitze eines Berges wurden die Tiefenwinkel alpha=32,3 Grad und beta=39,7 Grad nach der Spitze und dem Fußpunkt eines Turmes von der Höhe h=60m gemessen.

Ermittle die Höhe des Berges.

Answer 1

Angaben:

alpha=32,3°;

beta=39,7°;

h = 60m;

 

Winkelbeziehungen:

e = beta -alpha;

d = 90° +alpha;

 

Sinussatz:

sin(d) / s = sin(e) / h;

s = sin(d) / sin(e) * h = h * sin( 90° +alpha ) / sin( beta -alpha )

    = h *cos(alpha) / sin( beta -alpha );

 

Rechtwinkliges Dreieck:

b = s * sin(beta);

b = h *cos(alpha) * sin(beta) / sin( beta -alpha );

b = 60m *cos(32,3°)*sin(39,7°) / sin(39,7° -32,3°) = 251,53m;

 

lg JR

Answer 2

Dies ist die Antwort auf die ähnliche Frage " Trigonometrie ., kann keine Skizze anfertigen " ( Duplikat gelöscht ).

Da die Antwort etwas kürzer ist als Johanns habe ich Sie einmal hier hineingestellt.

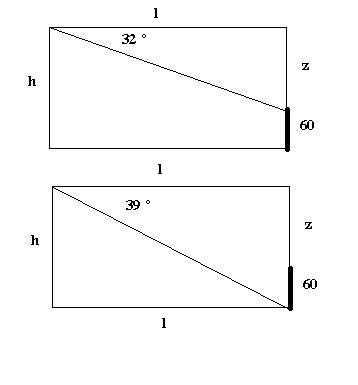
tan(32) = z / l
l = z / tan(32)

tan(39) = ( z + 60 ) / l
l = ( z + 60 ) / tan(39)

z / tan(32) = ( z + 60 ) / tan(39)
z = 60 / ( tan(39) - tan(32))
z = 324.47
h = z + 60
h = 384.47 m

auf dies Beispiel bezogen
z = 60 / ( tan(39.7) - tan(32.3))
z = 302.97 m
h = 362.97 m

Hier gibt es eine kleine Differenz zu Johanns Rechnung. Ich rechne beides noch einmal nach.

mfg Georg

 

 

Comments

Korrektur :

z / tan(32) = ( z + 60 ) / tan(39)
z = 60 * tan(32) / ( tan(39) - tan(32))
z = 202.75
h = z + 60
h = 262.75 m

auf dies Beispiel bezogen
z = 60 * tan(32.3 ) / ( tan(39.7) - tan(32.3))
z = 191.53 m
h = 251.53 m

  Beides dürfte somit stimmen.

  mfg Georg