Parameterwerte bei der der Graph nur ein Extremum besitzt

Question

Bei welchen Parameterwerten besitzt der Graph der angegebenen Funktion genau einen Extrempunkt ? Und für welche Werte besitzt der Graph keine Extrempunkte? 
ft(x) = 2x^3 + 3tx^2 + 6 tx + 1 
bitte mit ausführlichen erklärungen, vielen dank.

Answer 1

f_t(x) = 2x³ + 3tx² + 6 tx + 1 

hat die Grenwerte  ± ∞  für x → ± ∞

Es gibt also zwei Extremwerte oder keinen Extremwert.

Kein Extremwert:

f '(x) = 6·x² + 6·t·x + 6·t = 0   | : 6

x² + t·x + t = 0

x² + px + q = 0

pq-Formel:  p = t  ; q = t

x_1,2 = - p/2 ± $\sqrt{(p/2)^2 - q}$

x_1,2 =   ( ±√(t·(t - 4)) - t)/2 

Für t = 0 oder t = 4  wird die Wurzel 0, man hat also eine doppelte Nullstelle von f ' bei -t/2

→ Sattelpunkt und damit kein Extremwert.

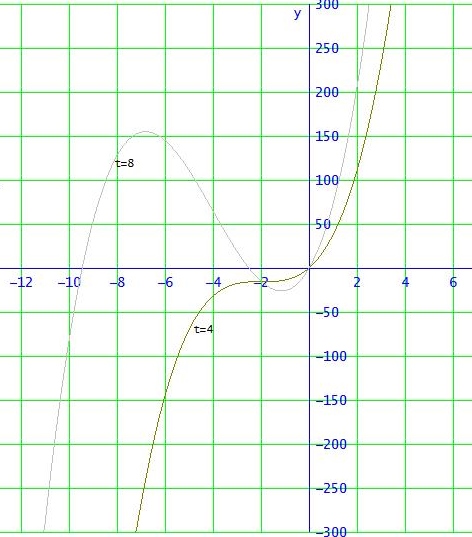
Hier eine Veranschaulichung:

Gruß Wolfgang

Comments

vielen dank! kann eine funktion dritten grades nie eine einzige Extremstelle haben?

---

Nein, sie kommt von -∞ und geht nach ∞  (oder umgekehrt)

wenn sie einen Hochpunkt hat, muss sie einen Tiefpunkt haben, damit sie wieder nach oben kommt (oder umgekehrt)