Erstelle eine Kurvendiskussion, 8. Grades Nullstellenberechnung, Extremwerte, Wendepunkt.

Question

f(x)= -x⁸+14x⁴-49 ich habe mittendrin einen Wurm drin und bitte um Hilfe.

Substituiert mit x⁸=z²

z= 7 Rücksubstitution ? wirklich x= ±\( \sqrt[4]{7} \) ?

Ich muss doch 8 Nullstellen haben, oder?

Bei den Extrempunkten habe ich für z dann 0; ±\( \sqrt[4]{7} \) und 49 raus.

Das kommt mir komisch vor.

Weiter bin ich noch nicht, brauche nur eine Info, ob ich falsch liege.

Danke

Answer 1

Eine Funktion 8. Grades kann 8 Nullstellen haben, muss sie aber nicht. Beispiel: y = x⁸

f(x) = -x⁸ + 14x⁴ - 49

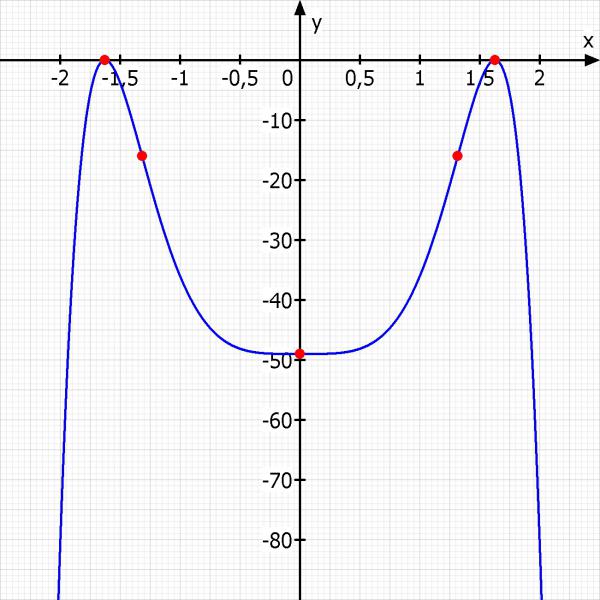
Die Funktion ist Achsensymmetrisch, daher brauche ich die Kurvendiskussion nur für alle positiven x machen. Negative x verhalten sich Achsensymmetrisch.

Nullstellen f(x) = 0
-x⁸ + 14x⁴ - 49 = 0 | Substitution z = x⁴
-z² + 14z - 49 = 0
z = 7
x = 7^1/4 = 1.627

Extremstellen f'(x) = 0
-8x⁷ + 56x³ = -8x³(x⁴ + 7) = 0
x = 0
x = 7^1/4
f(0) = -49 --> (0, 49)
f(7^1/4) = 0 --> (1.627, 0)

Wendestellen f''(x) = 0
-56x⁶ + 168x² = -56x²(x⁴ - 3) = 0
x = 0
x = 3^1/4
f(0) = -49 --> (0, 49)
f(3^1/4) = -16 --> (1.316, -16)

Skizze

Comments

Vielen Dank für die ausführliche Antwort.

Answer 2

\(-x^8 + 14x^4 - 49 = 0\)

Ohne Substitution:

\(x^8 -14x^4= -49\)

\((x^4 -7)^2= -49+49=0\)

\(x^4=7\)

\(x_1=\sqrt[4]{7}\)

\(x_2=-\sqrt[4]{7}\)

Es gibt noch 2 Lösungen ∈ ℂ.

Alternative:

\(f(x) = -x^8 + 14x^4 - 49\)

\(f'(x) = -8x^7 + 56x^3 \)

\( -8x^7 + 56x^3=0 \)

\( -x^7 + 7x^3=0 \)

\(x^3(-x^4+7)\)

\(x_1,_2,_3=0\)         \(f(0) =  - 49\)

\((-x^4+7)=0\) siehe bei Weg "Ohne Substitution"

Comments

Hast du schon mal etwas über die zweite binomische Formel gehört?

---

Es wurde mit Substitution gezeigt, und ich habe es ohne gemacht. Selbstverständlich geht es auch über die zweite binomische Formel.