Hallo Sonnenschein,
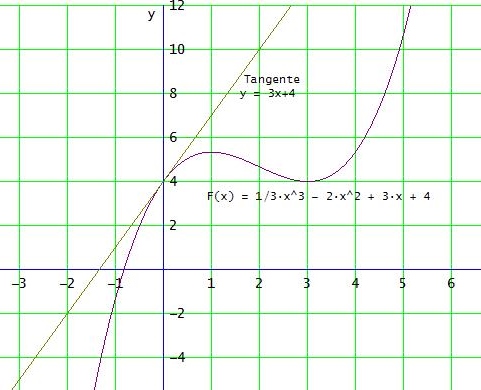
F(x)= 1/3x³ - 2x² + 3x + 4
die Konstante 4 verschiebt den Graph von F2(x) = 1/3x³ - 2x² + 3x einfach um 4 nach oben, weil die Funktionswerte F(x) an jeder Stelle x um 4 größer sind:
Tangente an der Stelle x=0:
F'(x) = x2 - 4x + 3 → Tangentensteigung F'(0) = mt = 3
F(0) = 4 ergibt den Berührpunkt B(0|4)
Die Gerade durch den Punkt P( xp | yp ) mit der Steigung m hat die Gleichung
y = m • ( x - xp ) + yp [ Punkt-Steigungs-Formel ]
t: y = 3 • (x - 0) + 4
t: y = 3x + 4
Gruß Wolfgang