Bestimme die Gleichung der Tangente an den Graphen von f(x)=1/x, welche parallel ist zu y=-1/4 x-2

Question

Hallo ich hoffe mir kann wer bei der Aufgabe helfen!

Sie lautet:

Bestimmen Sie die Gleichung der Tangente an den Graphen von f(x) = 1/x , welcher zu der Geraden mit der
Gleichung y =-1/4x - 2 parallel ist.

Answer 1

  f ( x ) = 1/x
  f ´ ( x ) = - 1 / x^2

  Die Tangente soll zur Geraden parallel sein : d.h. die gleiche Steigung haben

  - 1/4 * x  = - 1/ x^2
  x^3 = 4
  x = 1.59

  f ( 1.59 ) = 1/1.59 = 0.63

  P ( 1.59  l  0.63 )

  0.63 = 1.59 * -1/4 + b
  b = 1.03

  t (x) = -1/4 * x + 1.03

  mfg Georg

 ( Stimmt. Wurde überprüft )

Comments

Dankeschön! Nur noch eine Frage hast du bei der Gleichung y =-1/4x - 2 die minus 2 am Ende vergessen oder sind die irgendwie weggefallen?

---

  da die Tamgente und die Gerade nur parallel sein sollen müssen
sie nur die gleiche Steigung haben. Beide haben die Steigung -1/4.

  Die -2 sind für uns nicht von Bedeutung.

  Zeichne dir einmal alle 3 Funktionen ( die beiden Geraden sind schnell
gezeichnet, f=1/x auch ) in ein Koordinatensystem ein. Dann siehst du
die Zusammenhänge.

  mfg Georg

Answer 2

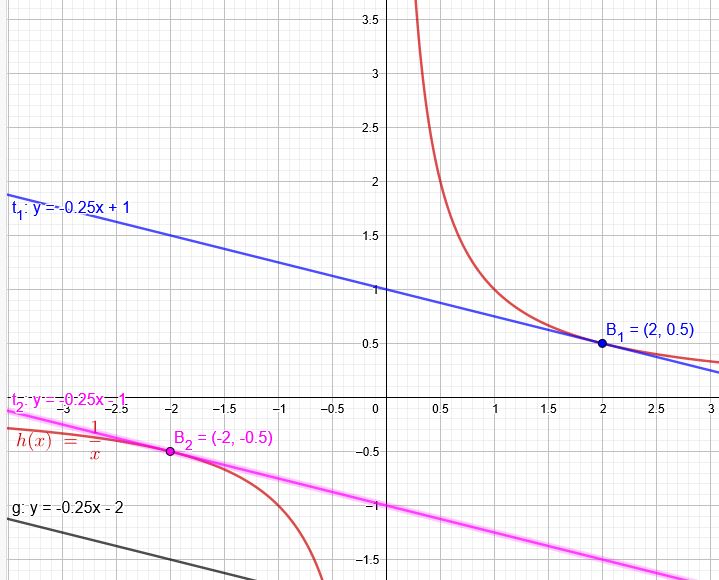
Bestimmen Sie die Gleichung der Tangente an den Graphen von \(f(x) = \frac{1}{x} \), welcher zu der Geraden mit der Gleichung \(y =\red{-0,25}x - 2\) parallel ist.

Lösung mit impliziter Differenzierung:

\(f(x,y)=x \cdot y\)

\(f_x(x,y)= y\)

\(f_y(x,y)=x \)

\(f'(x)= -  \frac{f_x(x,y)}{f_y(x,y)}=-\frac{y}{x}\)

\(\red{-0,25}= -\frac{y}{x}\)

\(y=0,25x\)  schneidet die Hyperbel  \(f(x) = \frac{1}{x} \) :

\(0,25x = \frac{1}{x} \) in den beiden Berührpunkten: \(B_1(2|0,5)\)  \(B_2(-2|-0,5)\)

Tangenten über die Punkt-Steigungsform:

\(\frac{y-0,5}{x-2}=\red{-0,25}\)

\(y=-0,25x+1\)

\(\frac{y+0,5}{x+2}=\red{-0,25}\)

\(y=-0,25x-1\)

Comments

@ Moliets:

Wenn du schon permanente Leichenfledderei an Altaufgaben praktizierst:

Kannst nicht etwas sorgfältiger arbeiten und dieses Konstrukt

\(y=0,25x\)  schneidet die Hyperbel  \(f(x) = \frac{1}{x} \) :   \(0,25x = \frac{1}{x} \) in den beiden Berührpunkten: \(B_1(2|0,5)\)  \(B_2(-2|-0,5)\)

einem eventuell interessierten Schülerpublikum nahezubringen?
Schließlich bezeichnest du dich doch als "Helfer".

@georgborn:

Möchtest du (mit dem zeitlichen Abstand von 11 Jahren) deine peinliche Antwort von 2013 (mit der Oberpeinlichkeit

Stimmt. Wurde überprüft )

nachbessern?