Für welchen ∈ Z ist f differenzierbar im Punkt 0?

Question

Ist f überhaupt differenzierbar?

Answer 1

f_n  ist stetig in x = 0   ⇔   n ≥ 1   (Edit nach Kommentar)

f_n'(x) =  (  n * x^n-1   für  x > 0

            (       0         für  x < 0

lim_x→0+  f '(x)  = 0 = lim_x→0-  f '(x)   ⇔  n > 1

→  f_n   ist  in x=0   differenzierbar  ⇔  n > 1

Gruß Wolfgang 

Comments

Warum ist f₁ nicht stetig?

---

Du hast natürlich mal wieder recht. Danke für den Hinweis. Vorher stand "für" statt "⇔" da. Habe es geändert.

---

f_n  ist stetig in x = 0   ⇔   n > 1
Das ist schon mal falsch.

lim_x→0+  f(x)  = 0 = lim_x→0-  f(x)   ⇔  n > 1
Das kann man zu deinen Gunsten als Schreibfehler ansehen.

Und jetzt machst du es entweder richtig (Gus hat es immerhin versucht) oder du beweist das hier

---

Der Schreibfehler war vor deinem Kommentar schon korrigiert.

Das hier, also 

https://www.mathelounge.de/418526/differenzierbarkeit-und-stetigkeit-von-funktionen

 ist eine allgemein bekannte Tatsache und wird bei solchen Beweisen einfach benutzt.      Wenn du anderer Ansicht bist, steht doch einer eigenen Antwort deinerseits nichts im Wege.

Answer 2

Nach links x ≤ 0 ist die Steigung 0.

nach rechts wäre zu zeigen das der Punkt x = 0
zum ersten Punkt der Funktion x^n eine Steigung
hat und diese identisch mit der Kurvensteigung ist ?
( na,hoffentlich stimmt das )

Dazu die Skizze

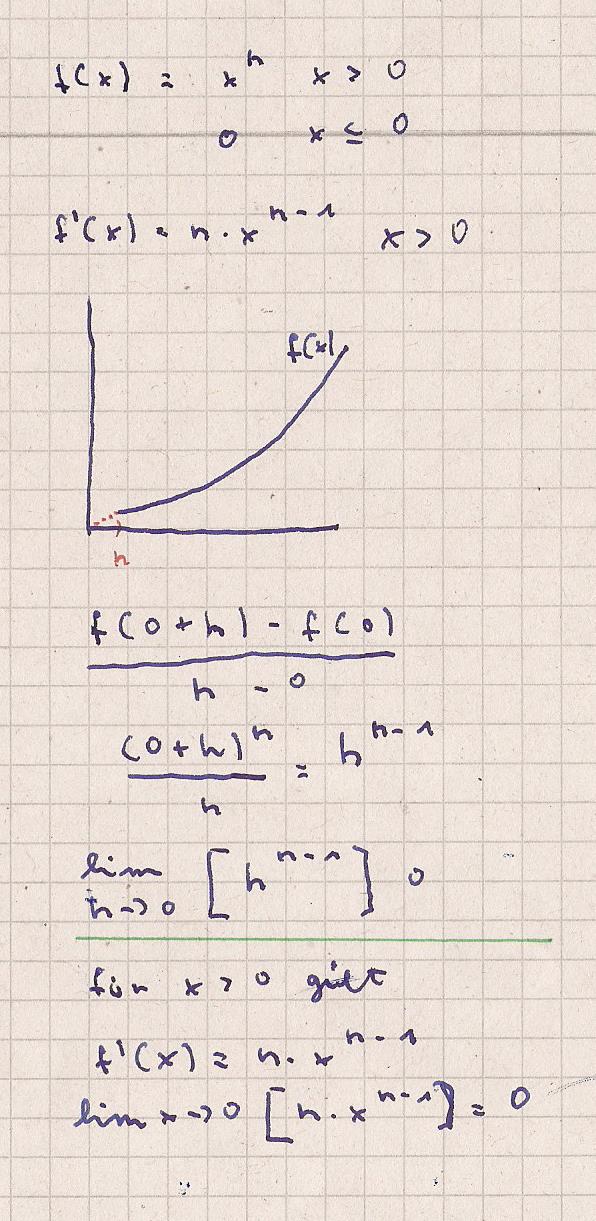
Der Differntialquotient ergibt für lim h −> 0 : 0
Die erste Ableitung der Funktion
lim x −> 0 : 0

Die Funktion ist also in x = 0 differenzierbar:

mfg

Comments

für n∈ ℤ mit  n ≤ 1  trifft das wohl nicht zu