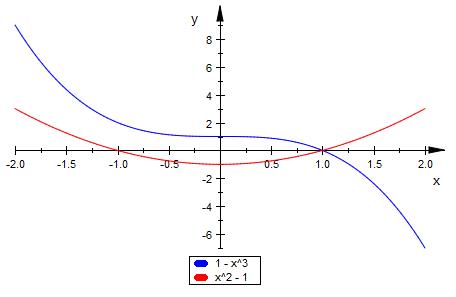
f(x)=1-x3 g(x)=x2-1
Weiß nicht wie ich die Schnittstellen von f(x)=g(x)
Eine Lösung kann erraten werden
x = 1
1 - x^3 = x^2 - 1
k ( x ) = x^3 + x^2 - 2
Eine Polynomdivision
x^3 + x^2 - 2 : x - 1
ergibt keine weiteren Schnittstellen
Es gibt nur 1 Schnittstelle
mfg Georg