Mittelpunkt & Radius eines Kreises bestimmen

Question

k= x^2 +y^2-8x+4y =30

Bestimme die Koordinaten des Mittelpunktes M sowie die maßzahl des Radius r für den Kreis k

Vielen Dank für Hilfe!

Answer 1

Hallo

quadratische Ergänzung ist das Stichwort!

$$x^2 +y^2-8*x+4*y =30$$

$$x^2-8*x+4^2+y^2+4y+2^2=30+16+4$$

$$(x-4)^2+(y+2)^2=50$$

Jetzt solltest du Mittelpunkt und Radius ablesen können und hoffentlich ähnliche Aufgaben selbst lösen

Gruß lul

Answer 2

x^2 + y^2 - 8·x + 4·y = 30

x^2 - 8·x + y^2 + 4·y = 30

x^2 - 8·x + 4^2 + y^2 + 4·y + 2^2 = 30 + 4^2 + 2^2

(x - 4)^2 + (y + 2)^2 = 50

M(4 | -2) ; r = √50

Answer 3

Nutze die Qudratische Ergänzung für \(x\)und \(y\) $$ k: x^2 +y^2-8x+4y =30 $$$$ (x^2 -8x + 16)-16 + (y^2+4y +4) - 4 =30 $$$$ (x -4)^2 + (y+2)^2 =30+16 +4 = 50$$$$ (x -4)^2 + (y+2)^2 = (5\sqrt{2})^2$$ daraus folgt, dass der Mittelpunkt \(M\) bei \(M=(4|-2)^T\) liegt und der Kreis \(k\) den Radius \(r=5\sqrt{2} \approx 7,07\) hat.

Obiges Bild zeigt den Kreis mit dem Kontrollpunkt \(P=(3|5)^T\). Die Probe zeigt, dass \(P\) die Kreisgleichung erfüllt.$$3^2 +5^2-8\cdot 3+4 \cdot 5 = 9 +25 - 24 + 20 = 30$$

Answer 4

allgemeine Kreisgleichung:

$$ k: (x-c)^2+(y-d)^2=r^2 $$

Der Mittelpunkt hat die Koordinaten (c|d)

$$ x^2-8x+y^2+4y=30 $$

Mittels quadratischer Ergänzung ergibt sich:

$$ (x-4)^2-16+(y+2)^2-4=30 $$

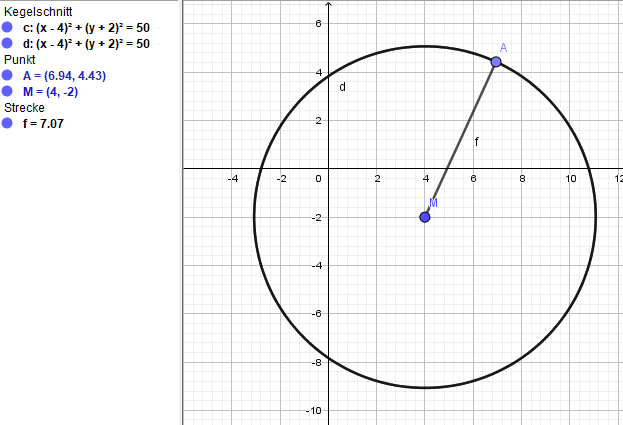
$$ (x-4)^2+(y+2)^2=50 $$

M (4|-2), Radius = 7,07

Gruß, Silvia