Zusammengesetzte Funktionen - Produktregel

Question

Gegeben ist die Funktion f mit f(x)=(x²+2x)*e^x

a) Bestimmen Sie die Gleichungen der Tangenten an den Graphen von f in den Schnittpunkten des Graphen mit der x-Achse.

b) Zeigen Sie, dass F mit F8x)=x²*ex eine Stammfunktion von f ist.

c) Berechnen Sie den Flächeninhalt, der vom Graphen von f unterhlab der x-Achse eingeschlossen wird.

Answer 1

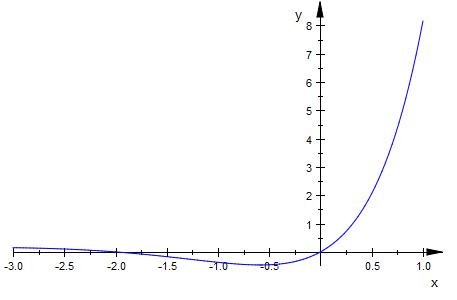
b) Zeigen Sie, dass F mit F(x)=x² * e^x eine
Stammfunktion von f ist.
Am einfachsten durch Ableitung

F(x)=x² * e^x
f ( x ) = 2x  * e^x + x² * e^x
f ( x ) = ( 2x + x² ) * e^x
bingo

a.)
Für einen Berührpunkt gilt
f ( x ) = t ( x )
f ´( x ) = t ´ ( x )

f(x)=(x²+2x)*e^x
f ´ ( x ) = ( 2x+ 2 ) * e^x + ( x² + 2x ) * e^x
f ´( x ) = ( x² + 4x + 2 ) * e^x

t ( x ) = m * x + b
t ´( x ) = m

Nullstellen ermitteln
f ( x ) = ( x² + 2x ) * e^x = 0
Satz vom Nullprodukt anwenden
e^x = 0 | nicht möglich
und
x² + 2x = 0
x * ( x + 2 ) = 0
x = 0
und x = -2
N1 ( 0 | 0 )
N2 ( -2 | 0 )

f ´( 0 ) = ( 0 ² + 4 * 0 + 2 ) * e ⁰
f ´( 0 ) = 2 * 1 = 2 = m
t1 = 2 * x + 0 = 2x

f ´( -2 ) = ( (-2) ² + 4 * (-2) + 2 ) * e ^-2
f ´( -2 ) = -0.27 = m

t ( x ) = m * x + b
t ( -2 ) = -0.27 * -2 + b = 0
0.54 =-b
b = - 0.54
t2 ( x ) = -0.27 * x - 0.54

c.)
Stammfunktion
F(x)=x² * e^x
[ F ( x ) ] zwischen -2 und 0
und absolut setzen

Bei Bedarf wieder melden

Comments

Die Antwort hat mir wirklich sehr geholfen und ich habe ale Rechenschritte nachvollziehen können. habe es jetzt auch verstanden. super erklärt! Nur ich verstehe c noch nicht so ganz :/ Was meinst du mit absolut setzen ?

Vielen Dank schonmal im voraus

---

F ( x ) = x² * e^x
0 ² * e ⁰ - ( (-2) ² * e^-2 )
0 - ( 0.54 )
- 0.54

Flächen sind stets positiv. Deshalb das
Ergebnis als Betrag nehmen.
| - 0.54 | = 0.54

---

Den Satz vom Nullprodukt wirst du wohl nie verstehen.

Answer 2

Hallo

a) Nullstellen kannst du hoffentlich mit x²+2x=0

ableitung nach Produktregel: (ex)'=ex,  (x²+2x)'=2x+2

also f'=e^x*(x²+2x+2x+2)

bei b) einfach F ableiten.

c) da du die Stammfkt aus b) kennst nur noch die Grenzen einsetzen.

Wo scheiterst du denn?

Gruß lul

Answer 3

Aufgabe a):

xxxxxxxxxxxxxxxxxxxxxxx