Lineare Algebra Steckbriefaufgaben

Question

ich brauche bei folgenden Aufgaben Hilfe:

a) Der Graph einer Funktion 5.Grades ist punktsymmetrisch zum Ursprung und besitzt im Punkt P(1/8) einen Sattelpunkt.

Mein Ansatz:

f(1) = 8

f'(1) =0

f''(1) = 0

f= 0

Problem: bekomme dass LGS nicht gelöst...

b) Der Graph einer Funktion dritten Grades hat dieselben Achsenabschnuttpunkte wie der Graph der Funktion g mit g(x) = 2x-x³. Beide stehen in P(0/0) senkrecht aufeinander.

Comments

bekomme dass LGS nicht gelöst

Dann sollte deine Frage lauten: Wie löst man das lineare Gleichungssystem

        a+c+e = 8
        5a + 3c + e = 0
        20a + c = 0.

Der Graph einer Funktion dritten Grades hat dieselben Achsenabschnuttpunkte wie der Graph der Funktion g

Hast du die Achsenschnittpunkte der Funktion g schon bestimmt?

Beide stehen in P(0/0) senkrecht aufeinander.

Das heißt

        f(0) = 0

        f'(0) = -1/g'(0)

---

Genau, soweit habe ich die Gleichungen heraus gefunden, aber wie löse ich die, da jetzt drei Variable aber nur zwei Gleichungen sind??

---

Hast du die Achsenschnittpunkte der Funktion g schon bestimmt?

---

wie berechnet man es nun mit dem Gauß -Verfahren???

---

Hast du schon die Achsenschnittpunkte der Funktion g bestimmt?

---

Hast du schon die Achsenschnittpunkte der Funktion g bestimmt?

Die werden nicht benötigt.

---

Die werden benötigt:

Der Graph einer Funktion dritten Grades hat dieselben Achsenabschnuttpunkte wie der Graph der Funktion g mit g(x) = 2x-x³.

---

Die werden benötigt: 

Nein.

Answer 1

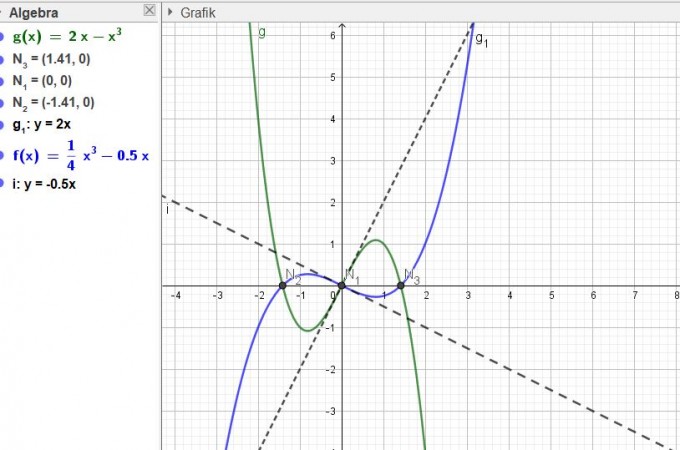
zu b)

$f\left( x \right)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+2bx+c\\g\left( x \right)=2x-x^3\\g'(x)=2-3x^2$

Nullstellen:

$$2x-x^3=0 \Longrightarrow x_1=0, x_2=\sqrt[]{ 2 },x_3=-\sqrt[]{ 2 }$$

Da die beiden Graphen im Punkt (0|0) senkrecht aufeinander stehen, gilt

$$g'(x)= -\frac{ 1}{ f'(x) }$$

$$g'(0)=2 \Longrightarrow f'(0)=-0,5\Longrightarrow c = -0,5\\f(0)=0\Longrightarrow d=0$$

Jetzt bleiben noch zwei Unbekannte a und b, die du mit den Gleichungen f($\sqrt{2}$) = 0 und f(-$\sqrt{2}$) = 0 lösen kannst.

Gruß, Silvia

Answer 2

Der Graph einer Funktion 5.Grades ist punktsymmetrisch zum Ursprung

Ansatz: f(x) = ax⁵ + bx³ + cx

Das sind nur 3 Unbekannte.

f(1) = 8

f'(1) =0

f''(1) = 0

Sind drei Gleichungen.

Answer 3

Plotlux öffnen

f₁(x) = 3x⁵-10x³+15xZoom: x(-2…2) y(-10…10)

Answer 4

zu b) Der Graph einer Funktion f dritten Grades hat dieselben Achsenabschnuttpunkte wie der Graph der Funktion g mit g(x) = 2x-x³. Beide stehen in P(0/0) senkrecht aufeinander.

(verwendeter Plotter: Google-Rechner)

Wie im Bilde zu sehen, entsteht die gesuchte Funktion f (rot) durch eine Streckung der Funktion g (blau) mit dem Faktor 0.25 in y-Richtung. Es gilt also $f(x)=0.25\cdot g(x)$. Warum? 

Ps: Ich korrigiere: Der Streckfaktor ist natürlich $-0.25$.