Hallo Roland,
Mir ist noch ein Beweis zum Conway-Kreis eingefallen, der nicht identisch mit dem von Spektrum-Rätsel ist.
Ausgehend von folgender Zeichnung:
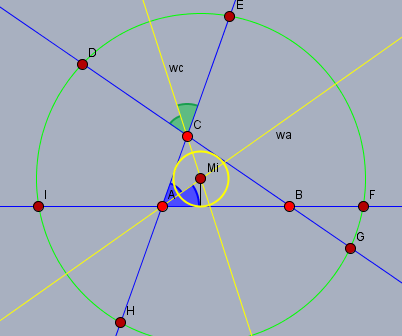
Aus \(|CE|=|CD|=c\) folgt: jeder Kreis, dessen Mittelpunkt auf der Winkelhalbierenden \(w_c\) liegt, der durch den Punkt \(E\) verläuft, geht auch durch \(D\). Aus \(|AE|=b+c=|AF|=c+b\) folgt: jeder Kreis, der auf der Winkelhalbierenden \(w_a\) liegt und durch \(E\) verläuft, geht auch durch \(F\). Daraus folgt, dass ein Kreis mit Mittelpunkt in \(M_I\), dem Schnittpunkt von \(w_c\) und \(w_a\), mit Radius \(r=|M_I D|\) durch die drei Punkte \(D\), \(E\) und \(F\) verläuft.
Das lässt sich für jedes Tripel von drei benachbarten Punkten zeigen. Folglich liegen alle sechs Punkte auf einem Kreis mit Mittelpunkt \(M_I\).
Gruß Werner