Lösung:
[spoiler]
n = 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
[/spoiler]
Beweis:
[spoiler]
In einem konvexen n-Eck sind die Innenwinkel \( < 180° \). Die Winkelsumme beträgt \( (n-2) \cdot 180° \).
Aus gleichseitigen Dreiecken (Innenwinkel \( 60° \)) und Quadraten (Innenwinkel \( 90°\)) können \( 60° \), \( 90° \), \( 120° \) und \( 150° \) Winkel konstruiert werden. Die maximal mögliche Innenwinkelsumme ist somit \( n \cdot 150° \).
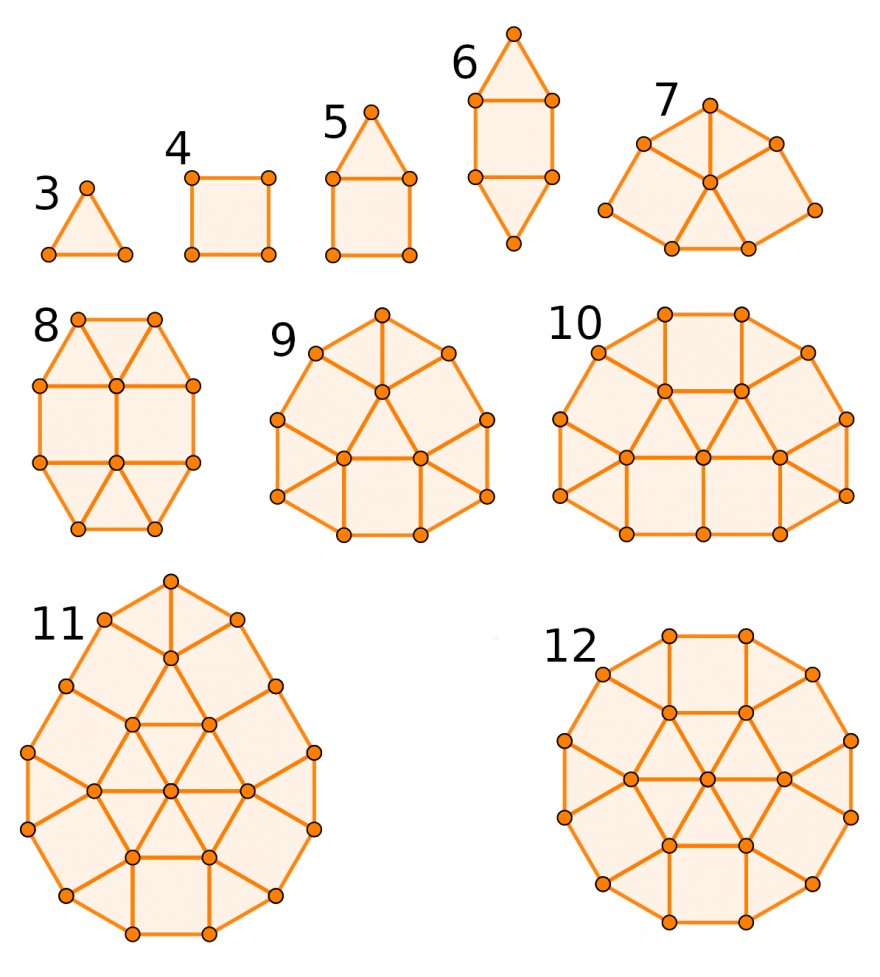
Der Existenzbeweis für \( n \in \{ 3,....,12 \} \) findet sich oben, als Grafik.
Für \( n > 12 \) kann es wegen \( n \cdot 150° < (n-2) \cdot 180° \) kein solches n-Eck geben.
[/spoiler]