Question

Betrachten Sie die Funktion f(x) = e^−0,5x − x.

• Wieviele Nulstellen besitzt f ?

• Überprfen Sie, ob die Bedingungen des Banachschen Fixpunktsatzes zur Berechnung der Nullstellen von f im Intervall I = [0, 1] erfullt sind.

Answer 1

Aloha :)

Du kannst die Gleichung zu einer Fixpunktgleichung der Form $x=f(x)$ umformen:$$e^{-0,5x}-x=0\quad\implies\quad x=e^{-0,5x}\eqqcolon f(x)$$

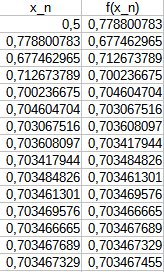
Für $x\in[0;1]$ gilt:$$\operatorname{max}|f'(x)|=\operatorname{max}|-0,5e^{-0,5x}|=\operatorname{max}\left(0,5e^{-0,5x}\right)=0,5<1$$Damit sind die Bedingungen des Banach'schen Fixpunktsatzes erfüllt und wir können die Nullstelle durch Interpolation ermitteln:$$x_{n+1}=f(x_n)\quad;\quad x_0=\frac{1-0}{2}=\frac{1}{2}$$

Answer 2

a)

Eine Nullstelle. ........

Answer 3

Wieviele Nulstellen besitzt f

f(x) = e^(- 0.5·x) - x = e^(- 0.5·x) + (- x)

Beide Summanden sind streng monoton fallend, daher ist auch die gesamte Funktion streng monoton fallend. Zusammen mit dem Verhalten im Unendlichen ergibt sich, dass die Funktion genau eine Nullstelle hat.

Answer 4

Du Nullstelle kann man nur mit einem Näherungsverfahren ermitteln oder der Lambert-Funktion.