Der Schatten der Kugel

Question

Aufgabe:

Durch eine punktförmige Lichtquelle $L$ wird von einer Kugel mit dem Radius $\mathrm{r}=10 \mathrm{~cm}$ ein Schatten auf dem Schirm $\mathrm{S}$ erzeugt.

Welchen Durchmesser hat der Schatten?

Problem/Ansatz:

Klein Tipp für den Durchmesser?

Comments

(ich habe frühmorgens Dummfug geschrieben)

...und tröste mich damit, dass ein anderer Benutzer dasselbe auch aufgeschrieben hat, es aber stehen lässt.

---

ich habe ehlrich aus vershen den Strecn gedrpückjt. ich versthe die Lösung NIHCT:

eine Frage wie veile wege gibt es überhaupt hier?

---

Warum vergibst du "Beste Lösung", für eine Lösung, die du nicht verstehst?

Wenn du meine Lösung (unten) nicht verstehst, bitte ich um eine Mail.

---

nein ich habe Aus Konzentration Problem aus versthen angklickt,

aber er mein 10 /50 = x /130?

1/50 * 130

0.2*130

26 ist Radius? aber woher bringt er das?

Zitat"Wenn du meine Lösung (unten) nicht verstehst, bitte ich um eine Mail" Ich habe diene ANtowrt NUR nUR gehsnen, es fehtl mir sehr scxhwer ALLES zu mekren, das belatet mich sehr

---

In Ordnung. Dann vielleicht später.

Answer 1

Hallo Zahri,

auf die Gefahr hin, dass Dich eine vierte Antwort verwirrt, antworte ich trotzdem ....

Schau Dir mal das Bild an, welches einen Schnitt der Szene aus Deiner Frage zeigt

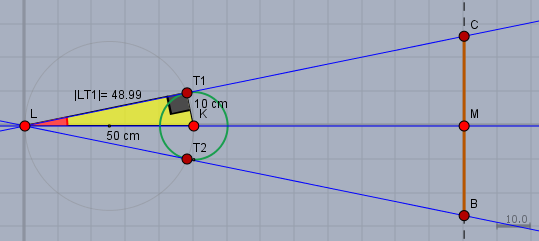
Dort findest Du das rechtwinklige Dreieck $LKT_1$ (gelb). In diesem Dreieck sind zwei Längen bekannt. Das ist die Seite$$|LK|= 50\,\text{cm}$$und der Radius der Kugel$$|KT_1|= 10\,\text{cm}$$Du kennst sicher den Satz des Pythagoras, mit dem man nun die Länge der dritten Seite berechnen kann. Es ist$$\begin{aligned}|LT_1|^2 +|KT_1|^2&= |LK^2|\\|LT_1|^2 + 10^2\text{cm}^2&= 50^2\text{cm}^2\\|LT_1|^2 + 100\,\text{cm}^2&= 2500\,\text{cm}^2&&|\,-100\,\text{cm}^2\\ |LT_1|^2&= 2400\,\text{cm}^2&&|\,\sqrt{}\\|LT_1|&=\sqrt{2400}\,\text{cm} \approx 48,99\,\text{cm}\end{aligned}$$Wir merken uns nun das Verhältnis der kleinen Kathete $|KT_1|$ des Dreiecks zur langen Kathete $|LT_1|$:$$\frac{|KT_1|}{|LT_1|} = \frac{10}{\sqrt{2400}}$$Der Zahlenwert selbst spielt keine Rolle, das kommt gleich.

Das nächste Bild zeigt nun ein weiteres rechtwinkliges Dreieck

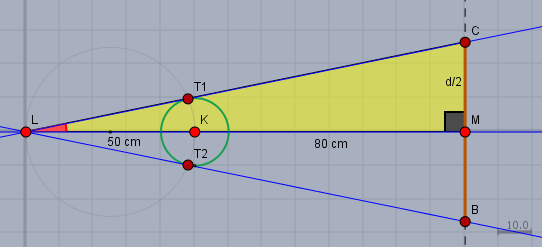
Links ist die Strecke $MC$ der halbe Durchmesser $d/2$ des Kugelschattens (braun). Dieses neue Dreieck sieht ganz ähnlich aus, wie das im ersten Bild, nur größer. Und es ist auch 'ähnlich' zum keineren Dreieck im mathematischen Sinne, weil die Winkel in diesem Dreieck alle genauso groß sind wie oben.

Das bedeutet, dass alle Verhältnisse von Seiten in diesem Dreieck genauso groß sind wie oben. Wir betrachten wieder das Verhältnis der kleineren Kathete $|MC|$ zur längeren Kathete $|LM|$$$\frac{|MC|}{|LM|}=\frac{d/2}{50\,\text{cm} + 80\,\,\text{cm}}=\frac{d/2}{130\,\text{cm}}=\frac{d}{260\,\text{cm}}$$Wir kennen aber bereits diese Verhältnis von oben - und das ist doch das gleiche, weil die Dreiecke ähnlich sind. Also ist doch$$\begin{aligned}\frac{d}{260\,\text{cm}} &= \frac{10}{\sqrt{2400}}\end{aligned}$$und dies ist eine Gleichung mit dem unbekannten Durchmesser $d$ des Kugelschattens und die kann man lösen$$\begin{aligned}\frac{d}{260\,\text{cm}} &= \frac{10}{\sqrt{2400}} &&|\,\sqrt{2400}=\sqrt{100}\cdot\sqrt{24}\\ \frac{d}{260\,\text{cm}} &= \frac{10}{10\cdot \sqrt{24}}\\ \frac{d}{260\,\text{cm}} &= \frac{1}{\sqrt{24}} &&|\, \cdot 260\,\text{cm} \\ d &= \frac{260}{\sqrt{24}}\text{cm}&&|\,\sqrt{24}=\sqrt{4}\cdot\sqrt{6}\\ d &= \frac{260}{2\cdot\sqrt{6}}\text{cm}\\ d &= \frac{130}{\sqrt{6}}\text{cm}\\d &\approx 53,07\,\text{cm}\end{aligned}$$Gruß Werner

Comments

Hallo Werner

ci meine wenn du die zweiten Radius( d/260) druch 130( untere Seite -->ML)  dividiert,dann musst auch muss du 10 durch 50( auch untere Seite KL) diviedieren, und NICHT 10 /48,99!!( obere SEite T1 L)

du dividierst 10( Radius von keinen Kreis) durch die obere Seite ( 48,99) dann dividierst du Radius( vom großrern kreis ) ducrch aber UNTERE Seite? wie geht das ?. wenn du die oberen lange Seite( CL) nicht kennst ,dann solltest du 10 /48,99 einmal=0.2

und dann das gleich bei größerem Kreis

10/50 = r2/130

0.2= r130

r=56

oder wenn du 10/48,99 ( T1 L obere Seiet ) dívideirst

dann solltest du auch r(d/2) AUCH durch OBERN Seite( CL)

( CL)  und NIHCT durch unteren Seite( ML) dividieren, denke ich.

Vielleicht hast du das übersehen.

oder bin ich durcheinander

---

Hallo Zahri,

es geht nicht um OBEN oder UNTEN! Die Dreiecke können doch alle gedreht und verschoben werden. Und wenn man die Dreiecke dreht oder verschiebt oder auch spiegelt, so ändern sich kein Verhältnis zwischen zwei Seiten.

Und es geht hier nur um das Verhältnis der kleineren zur längeren Kathete. Eine Kathete ist eine Seite im rechtwinkligen Dreieck, die an dem rechten Winkel anliegt.

schau Dir mal folgendes Bild mit den vielen Dreiecken an. Sie sind alle ähnlich zu dem besprochenen Dreieck oben.

Es geht immer nur um das Verhältnis der roten zur blauen Seite des Dreiecks. Und dies ist bei all diesen Dreiecken gleich.

Hol Dir mal einen Spiegel und schau Dir das Bild im Spiegel an. Auch da ist dieses Verhältnis immer gleich.

oder wenn du 10/48,99 ( T1 L obere Seiet ) dívidierst, dann solltest du auch r(d/2) AUCH durch OBERN Seite( CL) dividieren.

Nein - denn $CL$ ist die Hypotenuse des Dreiecks und die liegt dem rechten Winkel gegenüber! Sie hat mit dem Verhältnis der Katheten nichts zu tun.

---

hallo ich melde mich

---

Aha ,Aha

stimmtso?

Text erkannt:

$\operatorname{Dann} \sqrt{130^{2}-26,5^{2}}=127,27=\mathrm{m}$ $m=127,27$ ungeli. hr

---

stimmt so?

Ja ... alles was über dem Bild steht, hast Du richtig verstanden!

Das $\sqrt{130^2-26,5^2}$ macht keinen Sinn. Du hast leider nirgends geschrieben, was $m$ sein soll.

Die Strecke $|LM|=130\,\text{cm}$. Das ist in der Aufgabenstellung gegeben. Da die Strecke $|LM|$ senkrecht auf der Wand (dem Schirm) steht, muss jede andere Strecke von $L$ zur Wand länger sein. Also$$|LC| \gt |LM|$$und nach Pythagoras ist ($LC$ ist die Hypotenuse; das hat Du richtig beschriftet)$$|LC|^2=|LM|^2+|MC|^2 \\ \implies |LC|=\sqrt{|LM|^2+|MC|^2} = \sqrt{130^2 + 26,5^2}\,\text{cm} \approx 132,7\,\text{cm}$$Tipp: mache Dir eine genaue Skizze und messe Deine rechnerischen Ergebnisse in der Skizze nach.

---

ich melde mich morgen: war beim Trauam

---

Hallo werner, ich habe aus Versehen falsch,

habe mit Hand( es geht um Prinzip)

stimmt?

wenn ja dann habe kürze Frag.

Text erkannt:

$\begin{array}{rrr} & \sqrt{10^{2}+48,99^{2}} & b=130 \\ =50 & \sqrt{a+b^{2}}=c \\ & \therefore=50 & \sqrt{26,5^{2}+130^{2}} \\ & C=132,67 \\ & \text { ungefahr }\end{array}$

---

wenn ja dann habe kürze Frag.

das, was Du auf dem Bild skizzierst hast, ist alles richtig!

Wenn Du sonst noch eine Frage hast, so versuche diese bitte in einem einzigen Satz zu formulieren und mache ein '?' an das Satzende ;-)

---

Warum im kleinen Kreis kommt 90 oben oder beim größeren ( rechts) kommt der Winkel 90  UNTEN und nicht oben wie beim kleineren Kreis?

---

So

uns so

uns so

warum hast du den Winkel no1 ( unten)beim größeren Kreis gewählt und NICHT no 1( oben),ich  verstehe SCHON die Lösung aber verstehe nicht warum du nicht den oben Winkel ( no1) gewählt hast ? Hast du meine Frage verstanden?

Text erkannt:

(2)

---

Hallo Werner, hast du meine letzte Frage *(vor einem Tage gesehen) ? möchte gern eine Antwort.

---

Warum im kleinen Kreis kommt 90 oben oder beim größeren ( rechts) kommt der Winkel 90  UNTEN und nicht oben wie beim kleineren Kreis?

Der Radius des größeren Kreises ist weder bekannt noch gesucht. D.h. er interessiert gar nicht.

Genauso ist das rechtwinklige Dreieck (das letzte Bild in Deinem Kommentar), von dem Du den rechten Winkel mit einer (2) markiert hast, nicht von Interesse. Keine seiner Katheten ist bekannt oder gesucht. Lediglich die Hypotenuse $LM$ ist gegeben. (s. mein Bild wieter oben)

Das Dreieck $LMC$ ist interessant, da hier die längere Kathete gegeben ist und die kleinere gesucht ist. Weiter ist von diesem Dreieck das Verhältnis der Katheten bekannt. Und beim Dreieck $LMC$ ist der rechte Winkel eben beim Punkt $M$ - also im Bild unten und nicht oben.

---

ich lese in Ruhe morgen und melde mich

---

ehrlich habe ich deine Antwort ehrmals gelsen ------>>>  [[[[[[[[ Der Radius des größeren Kreises ist weder bekannt noch gesucht. D.h. er interessiert gar nicht.Genauso ist das rechtwinklige Dreieck (das letzte Bild in Deinem Kommentar), von dem Du den rechten Winkel mit einer (2) markiert hast, nicht von Interesse. Keine seiner Katheten ist bekannt oder gesucht. Lediglich die Hypotenuse $LM$ ist gegeben. (s. mein Bild wieter oben)Das Dreieck $LMC$ ist interessant, da hier die längere Kathete gegeben ist und die kleinere gesucht ist. Weiter ist von diesem Dreieck das Verhältnis der Katheten bekannt. Und beim Dreieck $LMC$ ist der rechte Winkel eben beim Punkt $M$ - also im Bild unten und nicht oben. ]]]]]]]]]

und versteh NUR Bahnhof warum du den rechte Wickeln bei großer Krieis NICHT WIE beim klinen KREIS OBEN gemacht , sondern hast du bei größeren Dreieck unten.

IM Buch frage er klar nach Durchmesser und es gibt dor auch größeren Kreis genau wie der kleiner kreis ,warum mache ich nicht dasselbe

---

... ich antworte Dir bis Sonntag Abend.

---

warum du den rechte Wickeln bei großer Krieis NICHT WIE beim klinen KREIS OBEN gemacht , sondern hast du bei größeren Dreieck unten.

Die Frage ist doch: was will man erreichen?

Gefragt ist doch nach der Größe des Schattens, den habe ich im Bild rot markiert. Ich kenne die Größe des Schattens, wenn ich die Länge der Strecke $CM$ kenne.

Und die Strecke $CM$ ist Kathete des rechtwinkligen Dreiecks $LMC$, mit dem rechten Winkel beim Punkt $M$ (rot).

Um das Dreieck $LMP$ (grün markiert) mit rechten Winkel bei $P$ (balu) braucht man sich nicht kümmern. Das hilft nicht bei der Lösung!

---

ich meine woher weiss du dass der Durchmesser der Schatten( shadow) ist diese rote Linie und NIXHT der Durchmesser des grösen Kreis? das meine ich , aber die Lösung verstehe schon. Wenn du denke gibt es keine Erklärung ,dann lassen, Weil ich versteh so : der Durchmesser bedeutet der Durchmesse vom großen Kreis, also → 26

---

ich meine woher weiss du dass der Durchmesser der Schatten( shadow) ist diese rote Linie und NICHT der Durchmesser des größeren Kreises?

Der Schatten befindet sich doch an der Wand, bzw. in der Aufgabe steht "auf dem Schirm". Und dieser Schirm ist flach. Da wo der große Kreis ist, befindet sich kein Gegenstand auf dem sich ein Schatten abbilden würde.

Durchmesse vom großen Kreis, also → 26

Da ist nicht richtig! Der Durchmessr des 'großen Kreises' ist kleiner als der Schatten. Die Strecke $|PM|$ ist kürzer als die Strecke $|CM|$.

Das Dreieck $MCP$ ist ja wieder ein rechtwinkliges Dreieck. $PM$ ist eine Kathete dieses Dreiecks und $CM$ die Hypotenuse. Und eine Kathete ist immer kürzer als die Hypotenuse. Man sieht das auch im Bild ....

---

Ich lese und melde mich

---

hallo Werner viellecht hilft wenn du diese Frage beantwortet
Dieser Schatten wie wird er erzeugt? und Wozu überhaupt?

---

Dieser Schatten wie wird er erzeugt?

Ist das eine ernst gemeinte Frage? Ok .. folgendes Bild

zeigt eine Lichtquelle $L$, die in alle Richtungen gradlinig Licht ausstrahlt. Ich habe vier Lichtstrahlen gezeichnet. Der oberste Lichtstrahl trifft den Schirm im Punkt 'Hell'. Da ist es hell, weil von der Lichtquelle hier Licht hinkommt.

Der nächste tangiert die Kugel (grün) gerade so in $T_1$. Er markiert die obere Schattengrenze $C$. Oberhalb von $C$ ist es hell. Der dritte Strahl trifft die Kugel im Punkt $H$. Da die Kugel keine Licht durchlässt, ist es dahinter dunkel - also im Punkt 'Dunkel' trifft keine Licht von $L$ den Schirm und wird nicht beleiuchtet - also dunkel.

Es bleibt dann dunkel bis zum Punkt $T_2$ bzw. in Verlängerung des vierten Strahls bis $B$. Lichtstrahlen, die unterhalb des vierten Strahls in Richtung Schirm laufen, können diesen beleuchten - also heller machen.

Den Bereich auf dem Schirm, der zwischen $C$ und $B$ liegt (der graue), nennt man den Schatten der Kugel.

und Wozu überhaupt?

es ist halt 'ne Schulaufgabe. Daran sollst Du wahrscheinlich üben, einfache geometrische Zusammenhänge formal und quantitativ zu beschreiben.

---

noch keine Frage: diese Schirm ist eine Tafel?

---

diese Schirm ist eine Tafel?

Ja - kann man so sagen. Es ist auf jeden Fall eine ebene Fläche, die durch die Lichtquelle im Punkt $L$ beleuchtet wird. Man kann auch sagen, es ist eine Wand. Ich habe den Ausdruck 'Schirm' gewählt, da er auch in der Aufgabenstellung benutzt wird.

---

diese Schatten sieht wie Quadrat oder Rechteck aus?

---

Hallo Zahri,

klick auf das Bild und rotiere die Szene mit der Maus. Der Schatten der Kugel ist rund!

---

krasse, jetzt ist klarer.ist jetzt erledigt .Thank alot

Answer 2

Alles in dm:

K1: (x-5)²+y²=1

K2: (x-2,5)² + y² = 2,5²

Koordinaten des oberen Schnittpunktes: x=$\frac{24}{5}$ ; y=$\frac{2·√6}{5}$.

Dann gilt nach einem Strahlensatz: $\frac{y}{x}$ = $\frac{z}{13}$ und daher: z=$\frac{13·√6}{12}$.

Die Schattengröße ist dann 2z.

Comments

wenn ich ovn ober eine Lösung fídne versuche IMER damit zu beschäftige, weil wenn nach unten ander Lösung, komme Durcheinander, deswegn versuche IMMER die erste Lösung von Oben zu verstehen wenn nicht dann gehen unten. die erste Lösung denk e jetzt vertshe aber ist das ein Gesetz?

---

Die erste Lösung verwendet einen Stahlensatz. Das tue ich auch. Aber die erste Lösung ist um 2% zu klein.

Answer 3

Hallo,

falls du Sinus und Co. kennst, kannst du es auch damit lösen.

Der halbe Öffnungswinkel des Kegels sei α, der Radius des Schattens R.

Dann ist

sinα=10/50=1/5=0,2 --> α≈11,54°

Außerdem gilt:

tanα=R/(50cm+80cm)

R=130cm•tanα≈26,536cm

Der gesuchte Durchmesser ist doppelt so groß.

D=2•R≈53,072cm

:-)

Comments

Deine Lösung gefällt mir auch.

---

Danke.

☺

---

Dann ist sinα=10/50=1/5=0,2 → α≈11,54°

ich würde drauf wetten, dass Zahri keine Ahnung hat was $\sin \alpha$ bedeutet.

---

Das mag schon sein, aber als genaue Lösung finde ich das am einfachsten.

---

"Mathematisch genau" müsstest du genauer definieren. Wenn man kein Wurzelzeichen mehr sieht, ist Genauigkeit fraglich. Ansonsten schön gemacht.

---

genau wäre IMHO $d=\displaystyle \frac{65}3\sqrt 6$, wenn man das idealisierte Modell unabhängig von seinen sonstigen physikalischen Eigenschaften betrachtet.

Answer 4

Du sollst hier den Strahlensatz anwenden

r/(50 + 80) = 10/50 --> r = 26 cm

Da nach dem Durchmesser gefragt wurde ist der berechnete Radius noch zu verdoppeln.

d = 2r = 52 cm

PS: Dann könnte man noch darauf hinweisen, dass der Strahlensatz hier nicht wirklich gilt, weil die Tangente an die Kugel nicht an beiden Seiten des Durchmessers anliegt.

Comments

ich beleibe bei erste Lösung, weilich zuerst damit angefangen habe

also, dies ist Strahelnsatz?

r er mein 10 /50 = x /130?

1/50 * 130

0.2*130

26 ist Radius?

stimmt so ? dann habe noch Frage

---

Du sollst hier den Strahlensatz anwenden

r/(50 + 80) = 10/50 → r = 26 cm

Was du hier machst, ist nur eine grobe Näherung.

Eine durch den Kugelmittelpunkt verlaufende Parallele zum Schirm schneidet die obere Begrenzung des Lichtkegels in einem Abstand vom Kugelmittelpunkt, der etwas größer ist als der von dir verwendete Kugelradius 10 cm.

---

also, dies ist Strahelnsatz?

r er mein 10 /50 = x /130?

1/50 * 130

0.2*130

26 ist Radius?

stimmt so ? dann habe noch Frage

---

Lies meinen Zusatz und setz dich wieder hin.

PS: Dann könnte man noch darauf hinweisen, dass der Strahlensatz hier nicht wirklich gilt, weil die Tangente an die Kugel nicht an beiden Seiten des Durchmessers anliegt.

---

26 ist Radius?

stimmt so ? dann habe noch Frage

Ja. 26 wäre hier der Radius. Was wäre denn deine Frage?

---

also stimmt dies erste Lösung:

ich weiss nicht mehr wo war diese Antwort( die Person)

jemand früher hat deise geschrieben-->

er mein 10 /50 = x /130?

1/50 * 130

0.2*130

26 ist Radius?

stimmt so ? dann habe noch Frage

also wenn das stimmt dann habe verstanden aber habe noch klein Frage

aber die Lösung erstmals trimmt?

---

Wie ich und auch andere Leute bereits gesagt haben, ist der von mir angewendete Strahlensatz nur näherungsweise richtig.

Ich gehe allerdings davon aus, dass ihr das exakt so lösen sollt, wie ich es aufgeschrieben habe.

Wenn du allerdings fleißig sein willst, könntest du versuchen genau zu erklären, warum es eben nicht exakt, sondern nur näherungsweise stimmt.

Und dann könntest du auch selber probieren, die Rechnung exakt zu machen.

---

warum straheln satz NIC HT EXakt? .--> 26

habe gerade die Lösung im Buch geguckt. Steht AUC 26!!!

---

Nicht exakt, weil in Schulbüchern immer auf das jeweilige Niveau des Schülers vereinfacht wird.

Etwas bessere Bücher nehmen eine Münze, statt einer Kugel, dann wird es besser allerdings bedingt durch die Dicke einer Münze auch eben auch nicht exakt.

Mach dir also nicht so viele Gedanken, du solltest wissen das berechnungsmodelle grundsätzlich nicht exakt sind. Ohnehin sind alle Anwendungsaufgaben mit fehlern belastet, denn wenn hier von einer Kugel mit dem Radius von 10 cm gesprochen wird, dann sind bereits die 10 cm mit einem gewissen Fehler behaftet. Der Radius der Kugel sollte sich daher im Intervall [9.5 ; 10,5[ befinden.

Und das wäre jetzt schon ein Fehler von ca. 5%

---

vertshe NICHT ganz was soll ich machen. nemeh diese Starhlsatz -_> 26 oder nicht?

---

Dass im Buch 26cm als Lösung steht, finde ich seltsam. Gesucht ist doch der Durchmesser und der wäre ja 2•26cm, also 52cm.

---

vertshe NICHT ganz was soll ich machen. nemeh diese Starhlsatz -_> 26 oder nicht?

Ja. Du nimmst den Strahlensatz und kommst auf einen Radius von 26 cm und damit dann auf einen Durchmesser von 52 cm.

Also 26 ist ein richtiges Zwischenergebnis allerdings nicht das Endergebnis.

---

ich eiss 26 ist r

und d= 2r=2*26=52 stimmt alles?

---

ich eiss 26 ist r

und d= 2r=2*26=52 stimmt alles?

Ja, das stimmt so.

---

ich finde diese Antwort, dich zuerst geschehen habe NICHT mehr: aber jetzt klar

---

warum straheln satz NIC HT EXakt? .--> 26
habe gerade die Lösung im Buch geguckt. Steht AUC 26!!!

dann ist dies ein dummes Buch! Wenn Du den Strahlensatz üben sollst, hätte man in der Aufgabe eine kreisförmige Scheibe statt der Kugel nehmen sollen.

Abgesehen davon wäre dies der Radius und gefragt ist aber nach dem Durchmesser - oder?

Was sagt denn Dein Lehrer bzw. Deine Lehrerin dazu?

Answer 5

@Zahri: Dann vielleicht erst mal in der Originalzeichnung mit dem Lineal und Bleistift die Streckenteilung bei 50 / 80 verlängern und den Mittelpunkt der Kugel suchen. Und das Ganze mit den Skizzen in den Antworten vergleichen. Am Bildschirm ist es schwierig die rechten Winkel sicher zu erkennen.