Zeigen Sie, dass die Hardy-Weinberg-Parabel tangential zu den Dreiecksseiten (in einem gleichseitigen Dreieck) verläuft.

Question

Aufgabe:

Zeigen Sie, dass die Hardy-Weinberg-Parabel tangential zu den Dreiecksseiten (in einem gleichseitigen Dreieck) verläuft.

Problem/Ansatz:

Hat irgendjemand eine Idee wie man an dieses Beispiele herangehen kann. Ich weiß wie die Parabel in einem gleichseitigen Dreieck aussieht finde jedoch keinen Ansatz für einen Beweis.

Comments

Du gibst ein bisschen wenig Informationen. Es hat vielleicht etwas mit dem De-Finetti-Diagramm zu tun. Dein Problem wird auf S. 29-33 in Foundations of Mathematical Genetics von Anthony W. F. Edwards thematisiert. Die Vorschau findest du bei Google-Books, such da nach "Hardy-Weinberg parabola".

---

Vielleicht sagst du zuerst, wie ihr die Hardy-Weinberg-Parabel genau definiert habt? Dann nimm das Dreieck symmetrisch zur y Achse mit Höhe 1.

lul

---

Vielleicht sagst du zuerst, wie ihr die Hardy-Weinberg-Parabel genau definiert habt?

Das sehe ich auch so. Gib doch bitte zuerst mal an, wie diese ominöse Parabel (von der ich bis vor 10 Minuten keine Ahnung hatte) definiert ist - oder wo wir eine solche Definition finden können !

(Oder gib uns mal alle Achsenschnittpunkte der Hayek-Karamanlis-Parabel an !)

---

Vielleicht hilft das weiter:

https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwjVzanPvJr-AhVAVfEDHXPFBPgQFnoECA0QAQ&url=https%3A%2F%2Fwww.math.uni-bielefeld.de%2F~sek%2Fbiomath%2Fleit11.pdf&usg=AOvVaw0YkEqCj2bvSM9d0K5Bil1X

Answer 1

Hallo,

Willkommen in der Mathelounge!

Ich unterstelle mal die Definition der Hardy-Weinberg-Parabel lautet wie folgt:$$y^2 = 4xz$$Wobei \(x\), \(y\) und \(z\) jeweils die trilinearen Koordinatem eines Punktes \(P\) auf der Parabel sind. Dann lässt sich das nach \(z\) umformen$$z=\frac{y^2}{4x}$$Im Punkt \(X\) (s. Skizze)

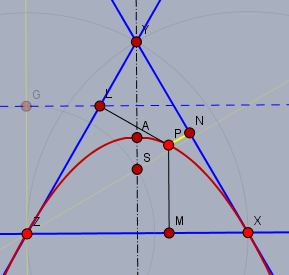
sind \(y=|PM|\) und damit auch \(z=|PN|\) (gelb) \(=0\). Wenn man nach \(z\) partial nach \(x\) und \(y\) ableitet, erhält man$$\frac{\partial z}{\partial x} = \frac{-y^2}{4x^2} \\ \frac{\partial z}{\partial y} = \frac{y}{2x}$$D.h. mit \(y=0\) sind auch die beiden Ableitungen \(=0\). Folglich muss die Tangente der Parabel im Punkt \(X\) in Richtung der Seite \(XY\) verlaufen, also tangential zur Dreiecksseite.

Gruß Werner

Comments

Alternative Lösung:

wenn man ein (kartesisches!) Koordinatensystem einführt, mit Urspring in \(Z\) und X-Achse durch \(ZX\), dann kommt man (nach einiger Rechnerei) auf die Parameterdarstellung der Parabel \(p\):$$\vec{p}(t)=2\begin{pmatrix} \frac{1}{3}\sqrt{3t}\\\sqrt{t}-t \end{pmatrix}$$\(t\) ist hier die trilineare Koordinate \(x\) von oben und läuft innerhalb des Dreiecks von \(0\) nach \(1\).

Ableitung nach \(t\) gibt$$\frac{\partial \vec{p}}{\partial t} (t)= \begin{pmatrix} \frac{1}{3}\sqrt{\frac{3}{t}} \\ \frac{1}{\sqrt{t}} - 2\end{pmatrix}$$Für \(t=1\) (Punkt \(X\)) ergibt sich $$\frac{\partial \vec{p}}{\partial t}(1) = \begin{pmatrix} \frac{1}{3}\sqrt{3} \\ -1\end{pmatrix}$$was identisch ist mit der Richtung der Dreiecksseite \(YX\).

---

Kurze Frage warum muss ich nach den Ableitungen y = 0 setzen?

---

Kurze Frage warum muss ich nach den Ableitungen y = 0 setzen?

nicht 'nach den Ableitungen' sondern grundsätzlich gilt doch, dass im betrachteten Punkt \(X\) - und um den geht's hier doch - die trilinearen Koordinaten \(y\) und \(z\) identisch zu \(0\) sind.

Die Hardy-Weinberg-Parabel verläuft durch die Punkte \(X\) und \(Z\).

---

Ok, ist das also deshalb, weil die Parabel in X dieselbe Steigung wie die Dreiecksseite haben muss.

---

Ok, ist das also deshalb, weil die Parabel in X dieselbe Steigung wie die Dreiecksseite haben muss.

Ja - genau