Hallo Roland,
Die Konstruktion der Strecken \(a\) und \(b\) kann wie folgt geschehen:
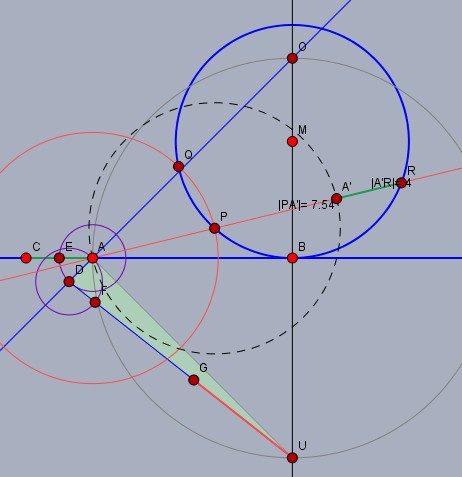
Man zeichnet die Tangente \(AB\) mit \(|AB|=12\) und das Lot in \(B\) auf dem der Mittelpunkt \(M\) (oberhalb \(AB\)) mit \(|MB|=7\) aufgetragen wird. \(K\) ist der Kreis um \(M\) mit Radius \(|MB|\) (blau).
Der Kreis um \(B\) (grau) mit Radius \(|BA|\) schneidet das Lot (schwarz) in \(O\) oberhalb der Tangente und \(U\) unterhalb. Man halbiere die Strecke \(4=b-a\) und der Kreis mit Radius \(4/2=2\) um \(A\) schneidet die Gerade \(AO\) in \(D\). Der Kreis um \(D\) mit Radius \(|DA|\) schneidet die Strecke \(DU\) in \(F\).
Der Punkt \(G\) halbiert die Strecke \(FU\) und da \(|GU|=a\) ist, wäre man hier bereits so gut wie fertig. Aber zur Kontrolle der Lösung zeichne man noch einen Kreis um \(A\) mit Radius \(|GU|=a\) (rot) der \(K\) in \(P\) und \(Q\) schneidet. Die Gerade durch \(AP\) (rot) ist die gesuchte Sekante, die \(K\) außer in \(P\) noch in \(R\) schneidet.
\(|AP|=a\) und \(|PR|=b\)
Als Add-on hier die gleiche Konstruktion in Desmos. Rechts oben kann man die Differenz \(b-a\) verändern.
Die analytische Lösung stützt sich (genau wie die konstruktive!) auf dem Sekanten-Tangenten-Satz ab. Es gilt:$$\begin{aligned}|AP| \cdot |AR| &= |AB|^2\\ a(a+b) &= 12^2 \land b-a=4 \\ \implies 2a^2 +4a &= 12^2 \\ (2a)^2 + 8a + 2^2 &= 2\cdot 12^2 + 2^2 \\ \left(2a+2\right)^2 &= (12\sqrt{}2)^2 + 2^2\end{aligned}$$Die letzte Zeile, so wie sie da steht, kann als Satz des Pythagoras im Dreieck \(\triangle DUA\) interpretiert werden (s.o.).
Die Lösung ist \(a= -1+\sqrt{73} \), das sollte nun jeder selber ausrechnen können. Und \(b\) ist um \(4\) länger ;-)
Gruß Werner