Hier eine Skizze
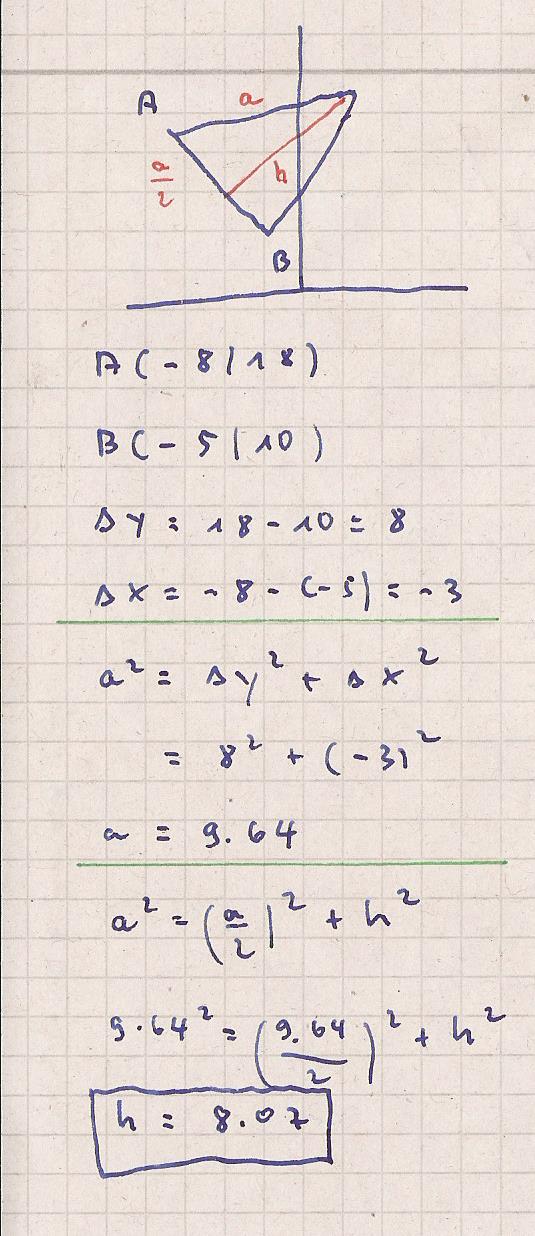
Zunächst wird der Abstand der Punkte A und B : delta x und delta y berechnet
und dann über den Pythagoras die Seitenlänge a.
a und a/2 sind bekannt und die Höhe h kann berechnet werden.
Bei den anderen Fragen fällt mir derzeit nur etwas Umständliches ein.
Mitte (AB) zwischen A und B berechnen
( -6.5 | 14 )
Steigung der Linie (AB) berechnen
m = Δ y / Δ x = -8 / 3 = -2.666
Die MIttelsenkrechte ( h ) entspricht der Normalen durch den Punkt AB
m ( normale ) = -1 / m = 0.375
14 = 0.375 * - 6.5 + b
b = 16.4375
n ( x ) = 0.375 * x + 16.4375
Die Gerade x = 0 ist die y-Achse. 16.4375 ist der y-Achsenabschnitt
und somit der gesuchte Schnittpunkt.