Schnittpunkte des Graphen mit der x-Achse berechnen

Question

Ich versuche gerade die Nullstellen eines Graphen zu berechnen, aber leider komme ich nicht voran.

Die Funktion lautet:

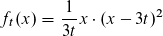
Zunächst habe ich die Klammer mit der Binomischen Formel ausmultipliziert:

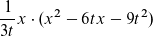
Um die Nullstellen zu berechnen habe ich mir als Ansatz f_t(x) = 0 notiert.

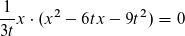
Dann habe ich mir überlegt mit dem Satz des Nullprodukten weiter zu rechnen.

1.Fall

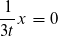
Aber wie löse ich nach x auf? Mich verwirrt nämlich die weitere Variable t.

MfG

Answer 1

Du hast es dir auch etwas zu schwer gemacht.

f(x) = 1/(3·t)·x·(x - 3·t)^2 = 0

Satz vom Nullprodukt: Ein Produkt wird null wenn mind. einer der Faktoren null wird.

1/(3·t) ist immer ungleich null

x = 0

(x - 3·t)^2 --> x = 3·t (2-fach)

Comments

Ich verstehe es leider noch nicht... Könntest du es mir erklären?

---

Was genau verstehst du nicht? Wenn ich das wüsste kann ich das bestimmt genau erklären.

Der Trick ist ja, wenn du eine Gleichung der Form

A·B·C = 0

hast, dann kannst du getrennt die Faktoren A, B und C null setzen.

---

Ich verstehe nicht wieso 1/(3·t) immer ungleich null ist und wie man noch auf x = 3*t kommt. Ich kann nichts mit der Variable t anfangen.

---

Ach, dann ist der 1. Fall

1/3t = 0,

der 2. Fall

x = 0

und der 3. Fall

(x - 3t)^2 = 0

Aber kann ich beim 1. Fall nicht nach t auflösen?

---

1/(3t) = 0

Ein Bruch wird null, wenn der Zähler null wird. Der Nenner darf ohnehin NIE null werden.

(x - 3t)^2 = (x - 3t)·(x - 3t) = 0

Auch dort gilt der Satz vom Nullprodukt. Allerdings sind ja beide Klammern gleich. Daher langt es sie einmal null zu setzen. Das ergibt dann aber immer eine 2-fache Nullstelle. Das ist eine Nullstelle ohne Vorzeichenwechsel. Also gleichzeitig ein Hoch oder Tiefpunkt.

Answer 2

Hey!

$$f^{ t }\left( x \right) =\frac { 1 }{ 3t } x(x-3t)²\quad |\quad f^{ t }\left( x \right) =0\\ \quad 0=\frac { 1 }{ 3t } x(x-3t)²\quad |\quad *\quad 3t\\ \\ 0\quad =\quad x(x-3t)²\quad |\quad Satz\quad von\quad Nullprodukt\quad -->\quad { x }_{ 1 }=0\\ \\ 0\quad =\quad (x-3t)²\quad |\quad a\quad und\quad b\quad in\quad 2.\quad Binomische\quad Formel\quad einsetzen\\ \\ 0\quad =\quad x²-6tx+9t²\quad \\ \\ $$

Jetzt musst du nur noch die Gleichung lösen.

Achtung t ist eine Zahl!

LG

Comments

Hallo Avenger,
die binomische Formel zum Schluß ist nicht
notwendig. Kürzer
( x - 3t ) ^2 = 0
daraus folgt
x - 3t = 0
x = 3t

---

Hallo Avenger,

als Tipp: Du kannst mit \text{text} in Latex schreiben. Das sieht dann etwas schicker aus, meiner Meinung nach.

Sähe dann so aus:

$$\text{Text!}$$

Gruß

Smitty